PHYSICS

Zobrazování optickými soustavami

May 22 2020 [Edit]

• Úvod
• Zrcadla
  • Rovinné zrcadlo
  • Kulové zrcadlo
    • Znaménková konvence poloměru křivosti a ohniskové vzdálenosti
  • Význačné paprsky pro konstrukci obrazu
  • Zvětšení optického zobrazení - $Z$
• Čočky
  • Spojky
  • Rozptylky
  • Optická mohutnost čočky $\phi$
  • Znaménková konvence poloměru křivosti
  • Zvětšení optického zobrazení
  • Znaménková konvence vzdálenosti obrazu
• Optické přístroje
  • Lidské oko
    • Vady lidského oka
  • Lupa
  • Mikroskop
  • Dalekohled

---

Úvod

• Zrcadlo
  • lesklá plocha
  • odráží se od něj světlo
  • zobrazování odrazem
  • dva typy: rovinné a kulové
• Čočky
  • zobrazování lomem
  • 2 typy: spojka a rozptylka
• Může vznikat obraz:
  • skutečný x zdánlivý
  • vzpřímený x převrácený
  • zvětšený x zmenšený x stejně velký
• Vytváření obrazu předmětu na základě zákonů fyziky
  • zákon přímočarého šíření světla
  • zákon odrazu a lomu
  • princip nezávislosti chodu světelných paprsků

---

Zrcadla

Rovinné zrcadlo

• Zobrazení odrazem na lesklé ploše
• Vzniká obraz: zdánlivý, vzpřímený, stejně velký, stranově převrácený
• Využití: zrcadlo v domácnosti, součást zobrazovací soustavy

Kulové zrcadlo

• Jejich plocha je část kulové plochy
• Oproti jiným kulovým zrcadlům nedeformují obraz
• Paraxiální prostor = prostor kolem optické osy, kde je zaručeno ideální zobrazení
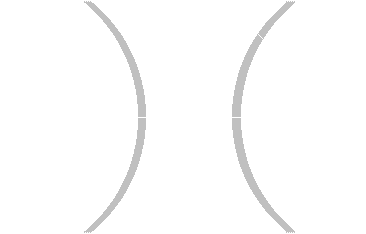
• Kulová zrcadla mohou být:
  • Dutá (obr. a) - zrcadlící plocha je na vnitřní straně vrchlíku
    • obraz je: skutečný, převrácený
    • využití: zvětšovací zrcátko u zubaře, součást zobrazovací soustavy
  • Vypuklá (obr. b) - zrcadlící plocha je na vnější straně vrchlíku
    • obraz je: zdánlivý, vzpřímený
    • využití: zmenšovací zrcadlo na křižovatce, součást zobrazovací soustavy

• $S$ - střed křivosti zrcadla
• $V$ - vrchol
• $F$ - ohnisko (střed úsečky $\lvert CV \rvert$ )
• $r$ - poloměr křivosti
• $f$ - ohnisková vzdálenost ($f = \frac{r}{2}$)
• $o$ - optická osa určená body $C$ a $V$

Znaménková konvence poloměru křivosti a ohniskové vzdálenosti

$r$ a $f$ mají před zrcadlem (u dutého zrcadla) hodnotu kladnou, za zrcadlem (u vypuklého zrcadla) zápornou.

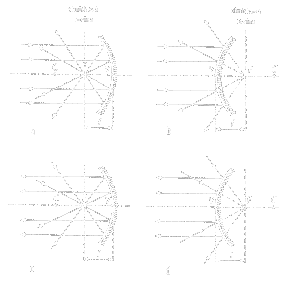
Význačné paprsky pro konstrukci obrazu

1. Paprsek procházející středem křivosti se odráží zpět do středu křivosti
2. Paprsek procházející ohniskem je po odrazu rovnoběžný s optickou osou
3. Paprsek rovnoběžný s optickou osou míří do ohniska

Zvětšení optického zobrazení - $Z$

• Bezjednotková veličina [1]
• Musíme brát v potaz znaménkovou konvenci
  • Veličiny $a$, $a'$ , $f$ mají v prostoru před zrcadlem kladnou hodnotu a za ním zápornou
  • Velikost předmětu a obrazu $y$, $y'$ má nad optickou osou kladnou hodnotu a pod ní zápornou

Zobrazovací rovnice:

$$Z = \frac{y’}{y} = - \frac{a’}{a} = - \frac{a’-f}{f} = - \frac{f}{a-f}$$

Podle velikosti $Z$ může být obraz:

• $Z > 0$ - vzpřímený
• $Z < 0$ - převrácený
• $\lvert Z \rvert > 1$ - zvětšený
• $\lvert Z \rvert < 1$ - zmenšený

Po úpravě rovnice dostáváme vztah:

$$\frac{1}{a} + \frac{1}{a’} = \frac{1}{f}$$

---

Čočky

• Parametry čoček jsou podobné jako zrcadel:
  • ohniska
  • vrcholy
  • středy křivosti
  • optický střed čočky

Tenká čočka = tloušťka čočky (vzdálenost bodů $V_1$ a $V_2$) je velmi malá, můžeme tedy říct, že tyto body splývají v optický střed čočky $O$

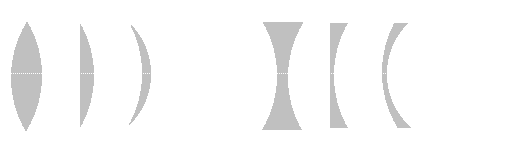
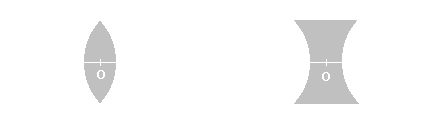
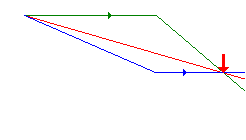
Spojky

• Svazek paprsků je po průchodu sbíhavý
• Význačné paprsky:
  • Paprsek jdoucí rovnoběžně s optickou osou se láme do ohniska
  • Paprsek procházející optickým středem čočky prochází beze změny
  • Paprsek procházející předmětovým ohniskem se láme a pokračuje rovnoběžně s optickou osou

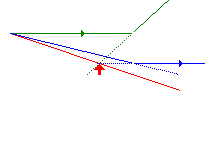
Rozptylky

• Svazek paprsků je po průchodu rozbíhavý
• Význačné paprsky:
  • Paprsek jdoucí rovnoběžně s optickou osou se láme do ohniska
  • Paprsek procházející optickým středem čočky prochází beze změny
  • Paprsek procházející předmětovým ohniskem se láme a pokračuje rovnoběžně s optickou osou

Optická mohutnost čočky $\phi$

$$\phi = \frac{1}{f} = \left ( \frac{n_{2}}{n_{1}} - 1 \right ) \left (\frac{1}{r_{1}} + \frac{1}{r_{2}} \right )$$

• $\phi$ - optická mohutnost čočky [D - dioptrie] nebo [m$^{-1}$]
• $n$ - index lomu prostředí
• $r = \lvert CO \rvert$ (pouze u tenkých čoček)

Znaménková konvence poloměru křivosti

Optické plochy vypuklé mají poloměr křivosti kladný a plochy duté záporný.

Zvětšení optického zobrazení

Vztahy jsou stejné jako u zrcadel:

$$Z = \frac{y’}{y} = - \frac{a’}{a} = - \frac{a’-f}{f} = - \frac{f}{a-f}$$

• $f$ - ohnisková vzdálenost ($f = \frac{r}{2}$)

Znaménková konvence vzdálenosti obrazu

Vzdálenost $a$ je kladná pře čočkou a záporná za čočkou. U $a'$ je tomu přesně naopak.

---

Optické přístroje

Lidské oko

• Oko lze považovat za spojnou čočku s měnitelnou ohniskovou vzdáleností
• Oko vidí předmět na různé vzdálenosti od oka, obraz se ale vytváří ve stále stejné vzdálenosti
• Obraz je skutečný zmenšený a převrácený

Vady lidského oka

Krátkozrakost (Léčí se rozptylkami)

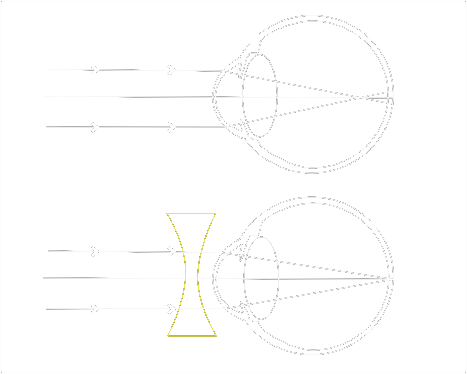
Dalekozrakost (Léčí se spojkami)

Lupa

• Nejjednodušší optický přístroj, tvořen jednou spojnou čočkou, jejíž ohnisková vzdálenost je menší, než vzdálenost od předmětu
• Vzniklý obraz je vzpřímený, zvětšený a zdánlivý
• Lupou lze dosáhnout maximálně 6-ti násobného zvětšení, při větším zvětšení se začínají projevovat optické vady čoček

Mikroskop

• Používá se ke zvětšení malých objektů, je tvořen minimálně ze dvou spojných čoček
• Skládá se ze dvou hlavních částí - objektiv a okulár
• Objektiv se nachází blíže k objektu, zobrazuje skutečný obraz
• Okulár je blíže k oku, vytvořený obraz posouvá dále od oka, abychom mohli lépe zaostřit

Dalekohled

• Optický přístroj, který zvětšuje optickou vzdálenost při sledování předmětů, jejichž vzdálenost od dalekohledu je několikanásobně větší než ohnisková vzdálenost
• Skládá se z objektivu a okuláru
• Například Keplerův dalekohled