PHYSICS

Paprsková optika

May 22 2020 [Edit]

• Úvod
• Optická prostředí
• Princip nezávislosti chodu světelných paprsků
• Odraz a lom světla
  • Lom světla - Snellův zákon
  • Úplný odraz světla
  • Disperze světla

---

Úvod

• Světlo
  • Elektromagnetické záření
  • Okem viditelné světlo má vlnovou délku od 390 do 760nm $\lambda = \frac{c}{f}$
  • Rychlost světla ve vakuu: $c \approx 3.10^{8}$ m.s$^{-1}$
• Paprsková optika
  • Optika zkoumá podstatu světla a zákonitosti světelných jevů
  • Paprsková optika zanedbává vlnovou podstatu světla

---

Optická prostředí

• Průhledné - nedochází k rozptylu světla.
• Průsvitné - částečný rozptyl, světlo se odráží různými směry.
• Neprůhledné - silná absorpce a odraz.
• Homogenní - stejné optické vlastnosti v celém objemu.
• Izotropní - rychlost šíření světla nezávisí na směru.
• Anizotropní - rychlost šíření světla závisí na směru

---

Princip nezávislosti chodu světelných paprsků

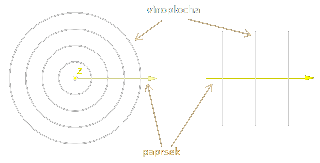
• Z bodového zdroje světla vycházejí paprsky všemi směry a navzájem se nijak neovlivňují
• Bodový zdroj světla si můžeme představit jako hmotný bod
• Jeho vlnoplochy mají tvar soustředných kružnic
• Ve velké vzdálenosti od bodového zdroje světla můžeme vlnoplochy považovat za rovinné

Odraz a lom světla

Paprsek dopadající na rozhraní dvou prostředí s odlišnými optickými vlastnostmi se z části odrazí a z části zlomí do druhého prostředí. Úhel dopadu je stejný jako úhel odrazu. Měří se od kolmice na rozhraní prostředí

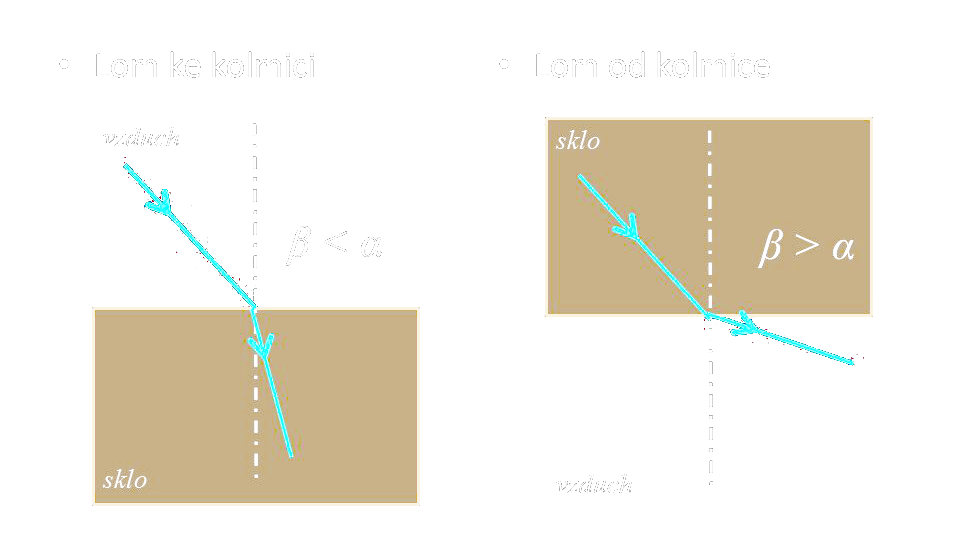
Lom světla - Snellův zákon

• Lom ke kolmici - nastává při lomu paprsku do opticky hustšího prostředí (větší index lomu)
• Lom od kolmice - nastává při lomu paprsku do opticky řidšího prostředí (menší index lomu)

$$n = \frac{c}{v}$$ $$\frac{\sin\alpha}{\sin\beta} = \frac{v_{1}}{v_{2}} = \frac{n_{2}}{n_{1}}$$

• $n$ - Index lomu - bezrozměrná veličina popisující šíření světla v daném prostředí (pro vakuum a vzduch $n = 1$)

Úplný odraz světla

K úplnému odrazu světla dojde v situaci kdy paprsek se odrazí pod větším úhlem, než je takzvaný mezní úhel a paprsek prochází opticky hustším prostředím. Paprsek lomu se láme do přechodu prostředí - úhel lomu je tedy 90°.

$$\alpha_{m} = \sin^{-1}\frac{n_{2}}{n_{1}}$$

• $\alpha_{m}$ - mezní úhel
• $n$ - Index lomu

Disperze světla

Rychlost světla v prostředí, kde $n>1$, závisí na frekvenci světla. Vlivem disperze se bílé světlo při lomu rozkládá na barevné složky. Jedním lomem vzniká monofrekvenční světlo určité barvy. Pro vícenásobný lom světla se používá optický hranol. Rovinné plochy hranolu, na kterých dochází k lomu světla svírají lámavý úhel - $\varphi$.

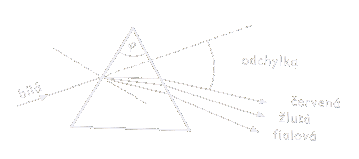
Optický hranol rozloží bílé světlo na spektrum všech barev monofrekvenčních světel. Tyto barvy jsou seřazeny od nejmenší hodnoty indexu lomu po největší (červená až fialová). Příkladem disperze světla z praxe je například duha. Při průchodu rozhraním optických prostředí se frekvence světla nemění a platí tedy:

$$f = \frac{c}{\lambda_{0}} = \frac{v}{\lambda}$$ $$\lambda = \frac{\lambda_{0}}{n}$$