PHYSICS

Vlnění

May 23 2020 [Edit]

• Mechanické vlnění
  • Rovnice postupného vlnění
  • Interference vlnění
    • Zvláštní případy interference
  • Odraz vlnění
  • Stojaté vlnění
  • Huygensův princip
  • Odraz vlnění
  • Lom vlnění
  • Polarizace vlnění
  • Ohyb vlnění
• Elektromagnetické vlnění
  • Zdroj elektromagnetického vlnění

---

Mechanické vlnění

Vyskytuje se ve všech látkách, jeho příčinou jsou vazby mezi částicemi:

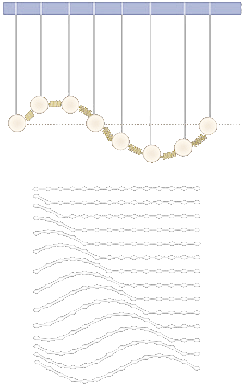
• Kmitání jedné částice přes vazbu rozkmitá jinou částici (pružné prostředí)
• Jednotlivé částice jsou jako mechanické oscilátory
• Vzniká postupné vlnění
• První kyvadlo udělá jeden kmit za dobu rovnou periodě $T$
• Za tuto dobu se vlnění rozšířilo rychlostí $v$, kterou se šíří do určité vzdálenosti, kterou nazýváme vlnová délka $\lambda$ (vzdálenost dvou bodů kmitajících se stejnou fází)

$$\lambda = v.T = \frac{v}{f}$$

• $\lambda$ - Vlnová délka - vzdálenost do které dospěje vlna za periodu $T$
• $T$ - Perioda - za jak dlouho vlnění vykoná vzdálenost jedné vlnové délky
• $v$ - Fázová rychlost

Vlnění příčné	Vlnění podélné
Je charakteristické pro: pružná pevná tělesa ve tvaru tyčí nebo vláken; pro vodní hladinu (např. elektromagnetické vlnění)	Vzniká v tělesech všech skupenství. Postupným vlněním podélným se v pružných látkách šíří např. zvuk

Rovnice postupného vlnění

$$y = y_{m}sin(\omega .t)$$

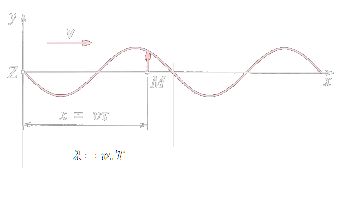
• $y$ - okamžitá velikost y
• $y_{m}$ - Amplituda - největší možné $y$
• $\omega$ - Úhlová rychlost

Postupné vlnění se šíří řadou hmotných bodů ze zdroje Z, který kmitá harmonicky. Rychlost vlnění je $v$. To znamená, že do bodu $M$ ve vzdálenosti $x$ od zdroje vlnění dospěje za dobu $\tau$.

$$\tau = \frac{x}{v}$$

Pro M bude tedy platit rovnice:

$$y = y_{m}sin\omega(t-\tau) = y_{m}sin\omega(t-\frac{x}{v})$$

Po dosazení $\omega = \frac{2\pi}{T}$ a $\tau = v.T$ dostáváme:

$$y = y_{m}sin2\pi(\frac{t}{T}-\frac{x}{\lambda})$$

Interference vlnění

• Děj, při němž se v určitém bodě prostředí, kterým se šíří vlnění, skládají okamžité výchylky dvou a více vlnění.
• Interferencí dvou stejných vlnění vzniká výsledné vlnění, jehož amplituda je největší v místech, v nichž se vlnění setkávají se stejnou fází (interferenční maximum) a nejmenší (popř. nulová) je v místech, v nichž se vlnění setkávají s opačnou fází (interferenční minimum)

O výsledku interference dvou vlnění rozhoduje fázový rozdíl vlnění $\Delta$$\varphi$. Určí se jako rozdíl fází obou vlnění:

$$\Delta\varphi = 2\pi(\frac{t}{T}-\frac{x_{1}}{\lambda}) - 2\pi(\frac{t}{T}-\frac{x_{2}}{\lambda})$$

Po úpravě a dosazení $d = x_{2} - x_{1}$ dostáváme:

$$\Delta\varphi = \frac{2\pi}{\lambda}d$$

Zvláštní případy interference

Nastává, když je fázový rozdíl roven celistvému počtu půlvln

• Sudý počet půlvln:
  • $d = 2k.\lambda$ $$
  • k = $\N \cup \{0\}$
• Lichý počet půlvln:
  • $d = (2k+1)\frac{\lambda}{2}$ $$
  • k = $\N \cup \{0\}$

Odraz vlnění

Na pevném konci se vlnění odráží s opačnou fází	Na volném konci se vlnění odráží se stejnou fází

Stojaté vlnění

Stojaté vlnění vzniká při neustálém harmonickém kmitání jednoho konce, na druhém konci se odráží a vzniká interference dvou vlnění, přímé a odražené, která postupují stejnou rychlostí a opačnými směry

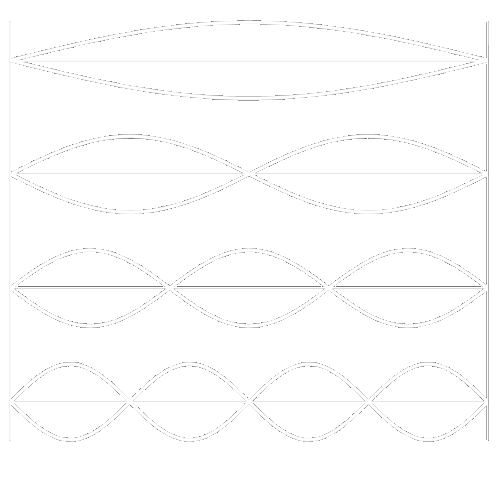
• Stojaté body se nazývají uzly
• Shluk bodů, které kmitají se nazývají kmitny

Huygensův princip

Každý bod vlnoplochy, do něhož dospělo vlnění v určitém okamžiku, můžeme pokládat za zdroj elementárního vlnění, které se z něho šíří v elementárních vlnoplochách.

Odraz vlnění

Odraz vlnění nastane, když vlnění narazí na neprostupnou plochu.

Zákon odrazu:

$$\alpha ’ = \alpha$$

Úhel odrazu vlnění se rovná úhlu dopadu

Lom vlnění

Při přechodu vlnění z jednoho prostředí do druhého se mění směr šíření vlnění

$$\frac{sin\alpha_{1}}{sin\alpha_{2}} = \frac{v_{1}}{v_{2}} = n$$

• $\alpha$ - úhel dopadu
• $v$ - rychlost vlnění
• $n$ - index lomu

Polarizace vlnění

Když body vlnění kmitají příčně, mohou kmitat v různých rovinách. Při polarizaci se z několika kmitových rovin vybírá jedna

Ohyb vlnění

Když vlnění narazí na překážku, která má rozměry přibližně stejně velké jako je vlnová délka, změní se směr šíření vlnění, aniž by vlnění přešlo do jiného prostředí – rozdíl od lomu

---

Elektromagnetické vlnění

Elektromagnetický oscilátor kmitá, probíhají v něm periodické změny energie

Energie, která se přenáší prostorem ve formě elektromagnetických vln, při elektromagnetickém vlnění se mění elektromagnetické pole, kmitají vektory $E$ (intenzita el. pole) a $B$ (mag. indukce) Např. světlo, radiové vlny, UV záření

Zdroj elektromagnetického vlnění

Zdrojem je elektromagnetický oscilátor (LC obvod, kmity molekul, změny elektromagnetického pole uvnitř atomů), pro šíření elektromagnetického vlnění jsou nutné jen změny elektrického a magnetického pole, proto se může šířit i vakuem.

Vztah pro okamžité napětí elektromagnetického vlnění:

$$u = U_{m}\sin \left ( \omega \left [ \frac{t}{T}- \frac{x}{\lambda} \right ] \right )$$