PHYSICS

Tepelné děje v plynech

May 18 2020 [Edit]

• Úvod
• Stavová rovnice ideálního plynu
  • Stavová rovnice ideálního plynu za stálé hmotnosti
  • Avogadrův zákon
• Tepelné děje v plynech
  • Izotermický děj
  • Izochorický děj
  • Izobarický děj
  • Adiabatický děj
• Vykonaná práce
  • Proměnlivý tlak
  • Izobarický děj
  • Kruhový děj

---

Úvod

Plyn v rovnovážném stavu lze charakterizovat: - termodynamickou teplotou $T$ - tlakem $p$ - objemem $V$ - počtem molekul $N$ (popřípadě hmotností $m$ nebo látkovým množstvím $n$)

---

Stavová rovnice ideálního plynu

rovnice, která vyjadřuje vztah mezi veličinami, které charakterizují plyn v rovnovážném stavu.

$$\begin{aligned} pV &= NkT \\ pV &= nRT \\ pV &= \frac{m}{M_m}RT \end{aligned}$$

• $T$ - Teplota [K]
• $k$ - Bolzmannova konstanta = $1,38.10^{-23}$ [J.K$^{-1}$]
• $R$ - molární plynová konstanta = $kN_A$ = 8, 31 [JK$^{-1}$]
• $N$ - počet částic [1]
• $n$ - látkové množství = $\frac{N}{N_A}$ [mol]
• $N_A$ - Avogadrova konstanta = $6,022141.10^{23}$ [mol$^{-1}$]
• $M_m$ - molární hmotnost = $A_r·10^{−3}$ [kg/mol]
• $A_r$ - relativní atomová hmotnost [1]

Stavová rovnice ideálního plynu za stálé hmotnosti

pokud $m = konst$ (plyn nepředává ani nebere částice z okolí) tak pro ideální plyn platí vztah

$$\frac{p_1v_1}{T_1} = \frac{p_2V_2}{T_2}$$

proto můžeme považovat $\frac{pV}{T}$ za konstantní. Skutečný plyn lze stavovou rovnicí pro ideální plyn popsat jen při nízkém tlaku a vysoké teplotě.

Avogadrův zákon

Různé ideální plyny o stejném objemu, teplotě a tlaku mají stejný počet molekul.

---

Tepelné děje v plynech

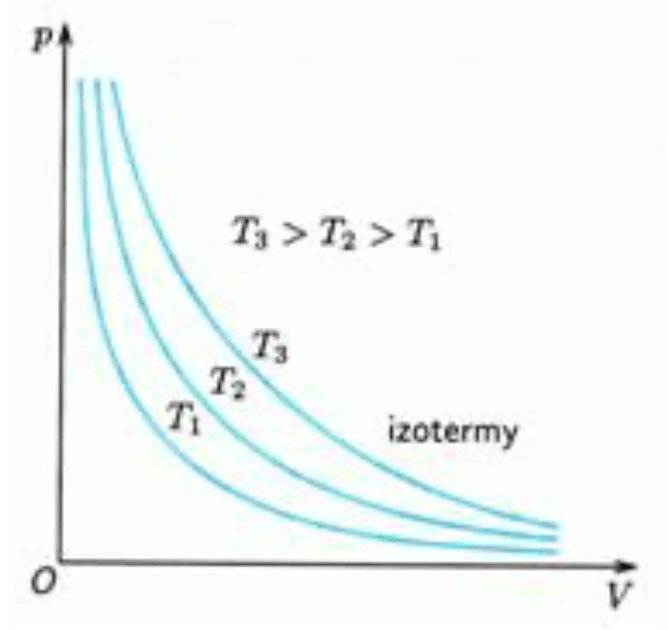
Izotermický děj

• Teplota je konstantní
• V praxi se dá konstantní $T$ udržet těžko. Šlo by to ale pomocí termostatu, který by při nepatrné výchylce teploty sepnul ohřívací těleso a to by dodával do plynu teplo.
• Boyleův-Mariotteův zákon:

$$\begin{aligned} pV &= konst \\ p_1V_1 &= p_2V_2 \\ m &= konst \end{aligned}$$

• Teplo přijaté plynem je rovno práci vykonané, změna vnitřní energie je 0

$$\begin{aligned} \Delta U &= O \\ Q_t &= W' \end{aligned}$$

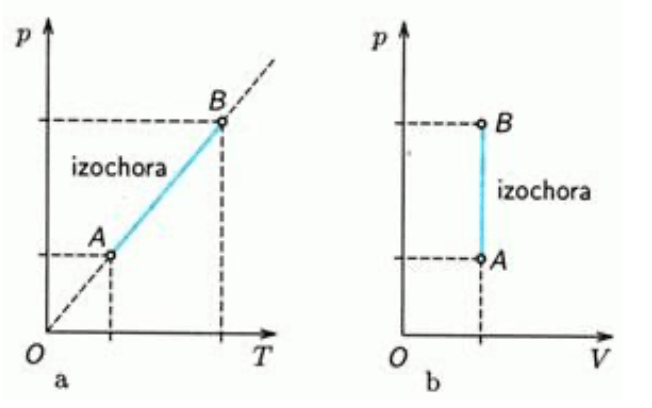
Izochorický děj

• Objem je konstantní
• V praxi se tento děj odehrává v plynu, který je v uzavřeném prostoru např. míč na který svítí slunce.
• Charlesův zákon:

$$\begin{aligned} \frac{p}{T} &= konst \\ \frac{p_1}{T_1} &= \frac{p_1}{T_1} \\ m &= konst \end{aligned}$$

• Teplo přijaté plynem je rovno přírůstku jeho vnitřní energie. Plyn nekoná práci.

$$Q_V = \Delta U = c_vm \Delta T$$ $$W' = 0$$

• $c_v$ - měrná tepelná kapacita plynu při stálém objemu

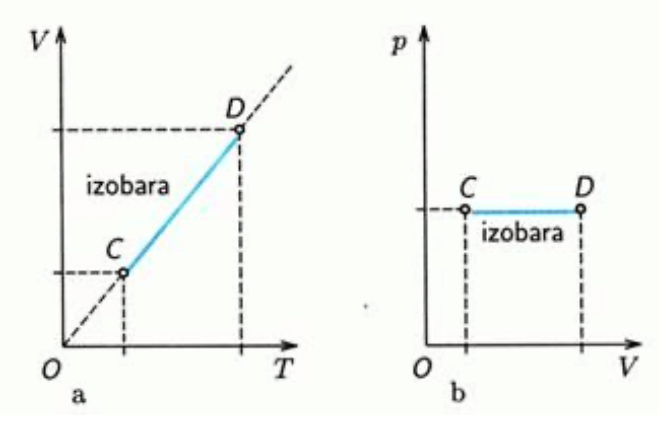
Izobarický děj

• Tlak je konstantní
• Gay-Lussacův zákon:

$$\begin{aligned} \frac{V}{T} &= konst \\ \frac{V_1}{T_1} &= \frac{V_1}{T_1} \\ m &= konst \end{aligned}$$

• Teplo přijaté plynem je rovno součtu přírůstku vnitřní energie a vykonané práce.

$$Q_p = \Delta U + W' = c_pm \Delta T$$ $$c_p = c_v + \frac{R}{M_m}$$

• $c_p$ - měrná tepelná kapacita plynu při stálém tlaku

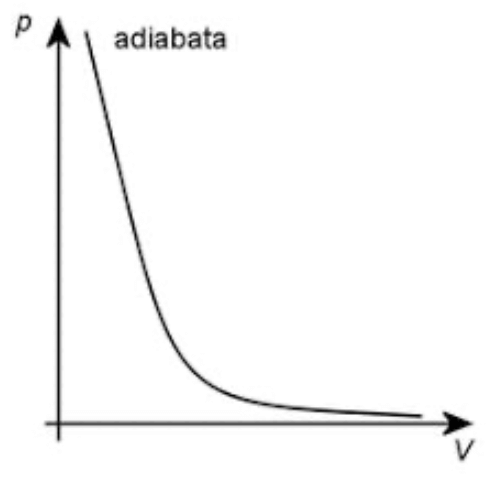
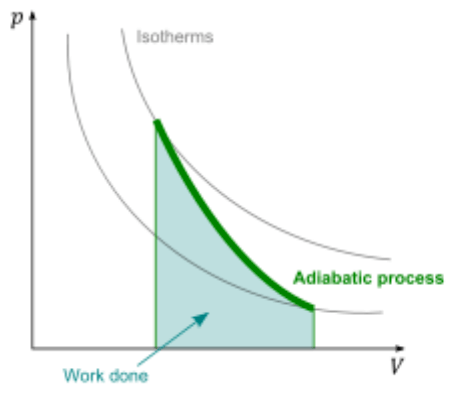
Adiabatický děj

• Neprobíhá tepelná výměna s okolím, což znamená, že $Q=0$
• Boyleův-Mariotteův zákon:

$$\begin{aligned} pV^\kappa &= konst \\ TV^{\kappa -1} &= konst \\ p^{1 - \kappa}T^k &= konst \\ m &= konst \end{aligned}$$

• $\kappa$ - Poissonova konstanta = $\frac{C_p}{C_v} = \frac{c_p}{c_v}$
• $C_p$ - tepelná kapacita při stálém tlaku
• $C_v$ - tepelná kapacita při stálém objemu
• $c_p$ - měrná tepelná kapacita při stálém tlaku

• $c_v$ - měrná tepelná kapacita při stálém objemu

• Teplo přijaté plynem je rovno 0, vnitřní energie je rovna vykonané práci.

$$\begin{aligned} Q &= 0 \\ \Delta U &= W \end{aligned}$$

---

Vykonaná práce

Proměnlivý tlak

$$W' = \int_{v_1}^{v_2} pdV = nRT \ln {\frac{V_2}{V_1}}$$

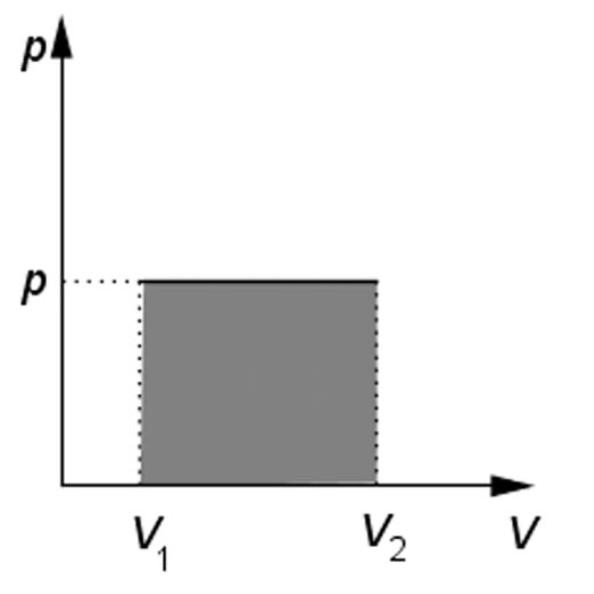
Izobarický děj

$W' = p\Delta V$

Kruhový děj

• konečný stav soustavy je roven prvotnímu stavu
• celková změna vnitřní energie je rovna 0

$$\Delta U = 0$$

• celková práce vykonaná plynem během jednoho děje je rovna celkovému teplu přijatému
• během tohoto cyklu (práce vykonaná plynem během kruhového děje je znázorněna plochou ohraničenou grafem kruhového děje)

$$Q = Q_1 - Q'_2$$ $$W' = Q$$

• ohřívač ($Q_1$) = těleso, od něhož přijme plyn teplo
• chladič ($Q'_2$) = těleso, jemuž odevzdá teplo

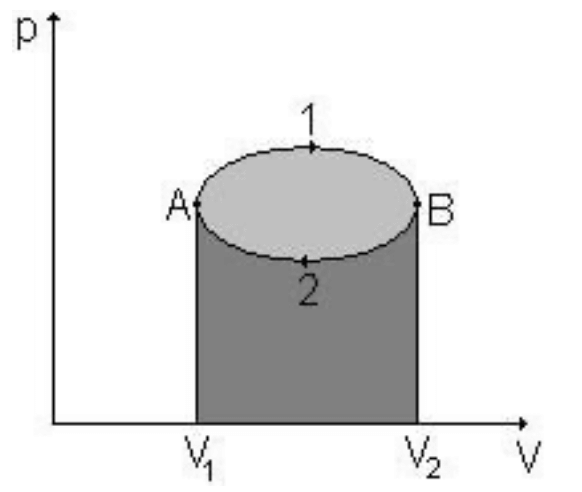
• účinost:

$$\eta = \frac{W'}{Q_1} = \frac{Q_1 - Q'_2}{Q_1} = 1 - \frac{Q'_2}{Q_1}$$