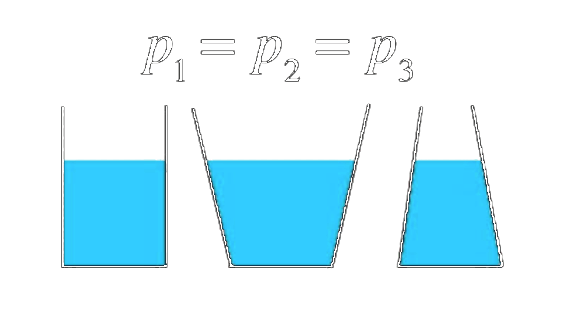PHYSICS

Hydrostatika

May 10 2020 [Edit]

• Úvod
  • Ideální plyn
  • Ideální kapalina
• Tlak v kapalinách a plynech
  • Pascalův zákon
  • Hydrostatický tlak
  • Hydrostatická tlaková síla
  • Hydrostatický paradox
  • Spojené nádoby
• Tlak vzduchu vyvolaný tíhovou silou
• Vztlaková síla v tekutinách
• Vztlaková síla v plynech
  • Odvození vztlakové síly
  • Archimédův zákon
• Chování těles ponořených v kapalině

---

Úvod

• Zabývá se vlastnostmi nepohybujících se kapalin
• Vlastnosti kapalin:
  • stálý objem
  • málo stlačitelné
  • vytvářejí vodorovný povrch
• Vlastnosti plynů:
  • snadno stlačitelné
  • velká vzdálenost mezi molekulami
  • objemem zaplňují celý prostor
• U kapalin i plynů lze posuzovat tekutost (viskozitu). Ta je zapříčiněna snadnou pohyblivostí částic. Právě proto nemají kapaliny ani plyny stálý tvar.
• Kapalinu i plyn budeme při odvození některých zákonitostí vnímat jako kontinuum, neboli spojité prostředí, což znamená že nepřihlížíme k jejich částicové struktuře.

Ideální plyn

• dokonale tekutý
• jeho molekuly mají nulové vnitřní tření
• dokonale stlačitelný

Ideální kapalina

• dokonale tekutá
• molekuly mají nulové vnitřní tření
• dokonale nestlačitelná

---

Tlak v kapalinách a plynech

• Značka $p$
• Jednotka – pascal [pa]
• Skalární veličina určující stav kapaliny
• Základní vzorec $p = \frac{F}{S}$
• Tlak měříme pomocí manometru
• Tlak může být vyvolán vnější nebo tíhovou silou

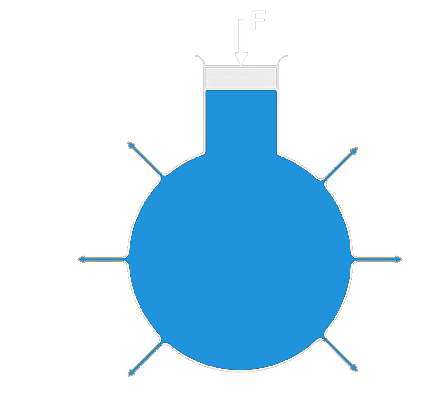
Pascalův zákon

Tlak vyvolaný vnější silou, působící na kapalinu v uzavřené nádobě je ve všech místech stejný.

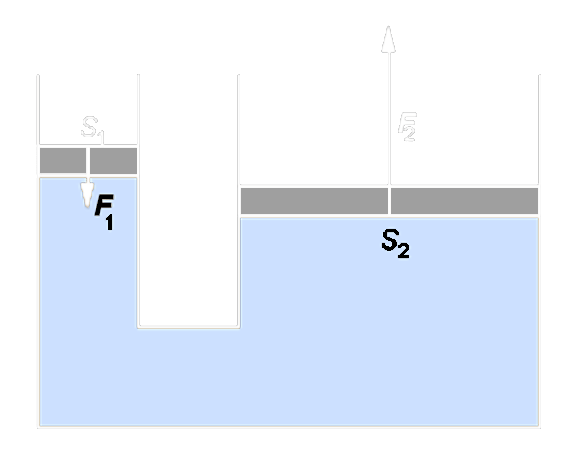
• Uplatnění pascalova zákona je především v hydraulických a pneumatických zařízeních (lisy, brzdy, zvedáky)
• Velikosti sil jsou ve stejném poměru jako obsahy ploch pístů

$$P = \frac{F_1}{S_1} = \frac{F_2}{S_2}$$

Hydrostatický tlak

Máme nádobu ve které vymezíme vodní sloupec o obsahu podstav $S_1$ a $S_2$. Podstava $S_1$ je na hladině a podstava $S_2$ je v hloubce $h$. Na plochu $S_1$ působí síla $F_1 = p_aS$, kde $p_a$ je atmosférický tlak. Na plochu $S_2$ působí síla $F_2$, která obsahuje sílu $F_1$ a tíhovou sílu kapaliny, tedy platí:

$$F_2 = F_1 + F_G$$ $$\downarrow$$ $$pS = p_aS+Sh\rho g$$ $$\downarrow$$ $$p = p_a + h\rho g$$

Rozdíl $p$ a $p_a$ označujeme jako hydrostatický tlak takže upravíme odvozený vzorec:

$$p_h =h\rho g$$

Hydrostatická tlaková síla

• V tíhovém poli země působí tíhová síla, výsledkem jejího působení je hydrostatická tlaková síla $F_h$
• Síla působí na dno i stěny nádoby
• Spočítáme jí jako hydrostatický tlak který působí na danou plochu:

$$F_h = p_hS$$ $$\downarrow$$ $$F_h = Sh\rho g$$

Hydrostatický paradox

Hydrostatická tlaková síla závisí na hloubce, hustotě kapaliny, gravitační konstantě a na ploše na kterou kapalina působí. Nezávisí na tvaru nebo objemu , proto je ve všech nádobách o různém objemu hydrostatická síla konstantní.

Spojené nádoby

Protože platí Pascalův zákon, je tlak ve všech místech kapaliny stejný, což dokazuje ta skutečnost, že ve spojených nádobách je kapalina v jedné výškové úrovni

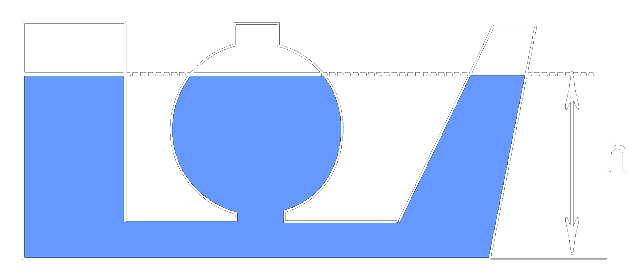
Kapaliny o různých hustotách mají na svém rozhraní stejný hydrostatický tlak

$$p_1gh_1 = p_2gh_2$$ $$\downarrow$$ $$\frac{p_1}{p_2} = \frac{h_1}{h_2}$$

---

Tlak vzduchu vyvolaný tíhovou silou

• Atmosférická tlaková síla $F_a$ je tíha atmosféry působící kolmo k dané rovině
• Atmosférický tlak $P_a$ je tlak vyvolaný atmosférickou tíhovou silou
• Běžná hodnota je 1013,25 hPa
• Tlak se měří barometrem - rtuťový barometr (Toricelliho pokus)
• Přetlak $\iff n > 1013,25$
• Podtlak $\iff n < 1013,2$

Vztlaková síla v tekutinách

• Tělesa ponořená do kapaliny jsou nadlehčována vztlakovou silou
• Vztlaková síla působí na těleso ze všech stran
• Má opačný směr než tíhová síla $F_G$

---

Vztlaková síla v plynech

• Okolní vzduch na tělesa působí nepatrně díky jeho nízké hustotě.
• Teplý vzduch, helium, vodík a další plyny mají nižší hustotu než vzduch.
• Toho lze využít v praxi:
  • horkovzdušné balony
  • vzducholodě nebo balónky

Odvození vztlakové síly

1. Na horní podstavu kvádru v hloubce $h_1$ působí hydrostatická tlaková síla $F_1 = Sh_1\rho g$
2. Na dolní podstavu kvádru v hloubce $h_2$ působí hydrostatická tlaková síla $F_2 = Sh_2\rho g$
3. Výslednice sil $F_1$ a $F_2$ je vztlaková síla

4. Z toho vyplývá:

   $$F_{vz} = F_2 - F_1 = Sh_2\rho g - Sh_1\rho g = S(h_1 - h_2)\rho g$$

5. A jelikož $h_2 - h_1 = \Delta h = h$, kdy $h$ je výška tělesa, platí:

   $$F_vz = Sh\rho g = V\rho g$$

Archimédův zákon

• Archimédés ze Syrakus byl řecký matematik, fyzik, filozof, vynálezce a astronom

Těleso ponořené do tekutiny, která je v klidu, je nadlehčováno silou rovnající se tíze tekutiny stejného objemu, jako je ponořená část tělesa.

• Důsledkem Archimédova zákona je různé chování těles v kapalině na které působí vztlaková síla a zároveň i síla tíhová $F_G = V\rho_tg$
• Chování těles v kapalině rozhoduje výslednice těchto sil

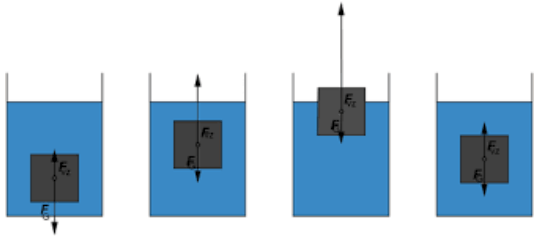
Chování těles ponořených v kapalině

1. Výslednice sil směřuje dolů
   • těleso klesá
   • hustota tělesa je vyšší
   • $\rho_t > \rho \implies F_G > F_vz$ $$
2. Výslednice sil směřuje nahoru
   • těleso stoupá
   • hustota tělesa je nižší (na hladině jsou síly v rovnováze).
   • $\rho_t < \rho \implies F_G < F_vz$ $$
3. Výslednice sil je nulová
   • těleso se volně vznáší v kapalině
   • hustoty se rovnají
   • $\rho_t = \rho \implies F_G = F_vz$ $$