PHYSICS

Kvantová fyzika

May 20 2020 [Edit]

• Elektromagnetické záření
• Záření černého tělesa
  • Wienův zákon posunu
• Kvantová hypotéza
• Foton
• Fotoelektrický jev
  • Závislosti fotoelektrického jevu
• Comptonův jev
• Vlnové vlastnosti částic
• Fotometrie

---

Elektromagnetické záření

• Záření (radiace) je šíření energie prostorem
  • chová se jako vlnění a zároveň jako proud částic
• Elektromagnetické záření je proces opakujících se přeměn elektrického a magnetického pole, které se šíří prostorem
  • je to příklad nestacionárního pole
  • tvoří jej dvě neoddělitelné složky:
    • Elektrická
    • Magnetická

---

Záření černého tělesa

Černé těleso je fyzikální model ideálního tělesa, které neodráží ani nerozptyluje dopadající elektromagnetické záření, veškeré záření pohlcuje. Modelem černého tělesa je dutina, do které proniká záření, ale nevystupuje ven.

Při určité teplotě vyzařuje černé těleso do prostoru elektromagnetické záření o různé intenzitě.

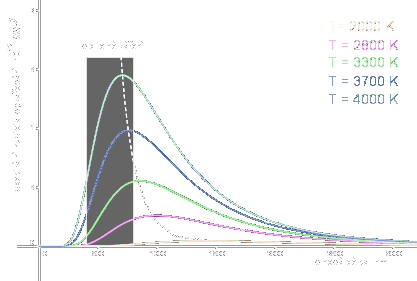
Z grafu je vidět různá intenzita elektromagnetického záření v závislosti na vlnové délce.

• Spektrální hustota intenzity vyzařování - $H$ -fyzikální veličina, která určuje jaká část celkové energie vyzářené zdrojem přísluší záření o vlnové délce $\lambda$ při teplotě zdroje $T$

Wienův zákon posunu

Určuje jakou vlnovou délku vyzařuje předmět o určité teplotě:

$$\lambda = \frac{b}{T}$$

• $b = 2,9.10^{-3}$ mK (konstanta)
• $T$ - teplota

---

Kvantová hypotéza

• Max Planck - zakladatel kvantové teorie
• Nazýváme ji hypotézou, ale už je potvrzena

Elektromagnetické záření vyzařované jednotlivými atomy tělesa není vyzařované spojitě, ale po určitých minimálních dávkách – kvantech energie.

Energie nemůže být libovolně malá, neboť je kvantována a její kvantum závisí na frekvenci záření.

---

Foton

• Energie záření je vysílána, šířena i pohlcována po určitých kvantech, které se nazývají fotony
• Elementární částice s nulovou klidovou hmotností
• Ve vakuu dosahuje rychlosti světla
• Energie fotonu (kvanta záření) se dá vyjádřit vztahem:

$$E = h.f$$

• $h$ - Planckova konstanta = 6,626.10$^{-34}$ [J.s]
• $f$ - frekvence [Hz]

---

Fotoelektrický jev

• Dopadající záření uvolňuje z některých látek elektrony, které pak mohou vytvářet elektrický proud v obvodu
• Důkaz kvantové povahy elektromagnetického záření
• Zákonitosti tohoto jevu vysvětlil Albert Einstein, který za to dostal Nobelovu cenu
• Část energie se spotřebuje na uvolnění tohoto elektronu z obalu a část se přemění na kinetickou energii elektronu, který vylétne z látky.

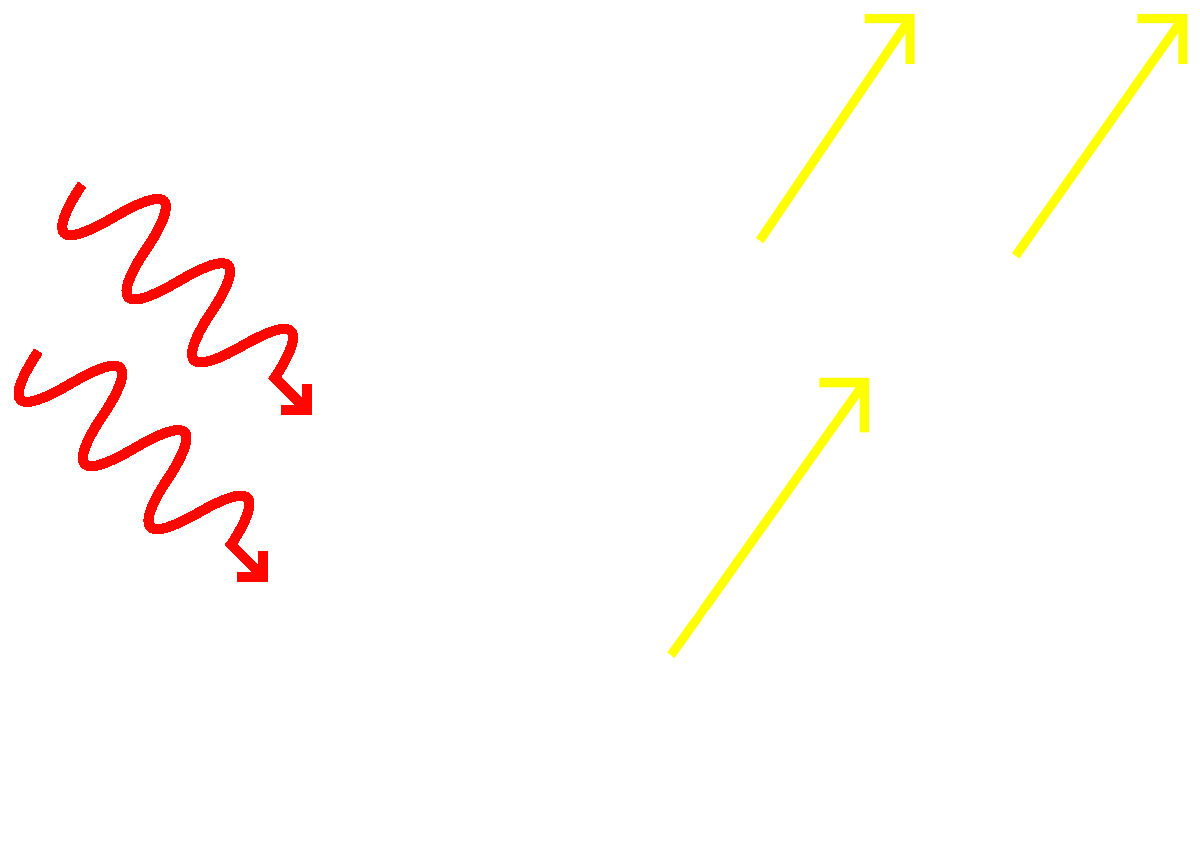
• Platí zde zákon zachování energie
• Einsteinova rovnice fotoelektrického jevu:

$$h*f = W_{v} + E_{k}$$

Z tohoto vztahu si můžeme vyjádřit mezní frekvenci záření (frekvence nutná k uvolnění elektronu z vazby):

$$f_{mez} = \frac{W_{v}}{h}$$

• $W_{v}$ - energie potřebná potřebná pro uvolnění elektronu z obalu [J]
• $h$ - Planckova konstanta = 6,626.10$^{-34}$ [J.s]
• $f$ - frekvence [Hz]

• Druhy:
  • Vnější fotoelektrický jev – probíhá na povrchu látky, elektrony se uvolňují do okolí
  • Vnitřní fotoelektrický jev – uvolněné elektrony zůstávají v látce jako vodivostní elektrony (polovodiče)

Závislosti fotoelektrického jevu

• Pro každý kov existuje určitá mezní frekvence (a jí odpovídající mezní vlnová délka) taková, že se elektrony uvolňují pouze při ní a vyšších frekvencích. Jestliže je frekvence záření menší než mezní frekvence, fotoelektrický jev nenastává.
• Je-li frekvence záření vyšší než mezní, bude proud protékající obvodem úměrný intenzitě záření.
• Energie elektronů, které se z kovu uvolňují, roste lineárně s frekvencí záření.
• Tedy zvýšením intenzity záření se zvýší počet uvolněných elektronů, ne však jejich energie.

---

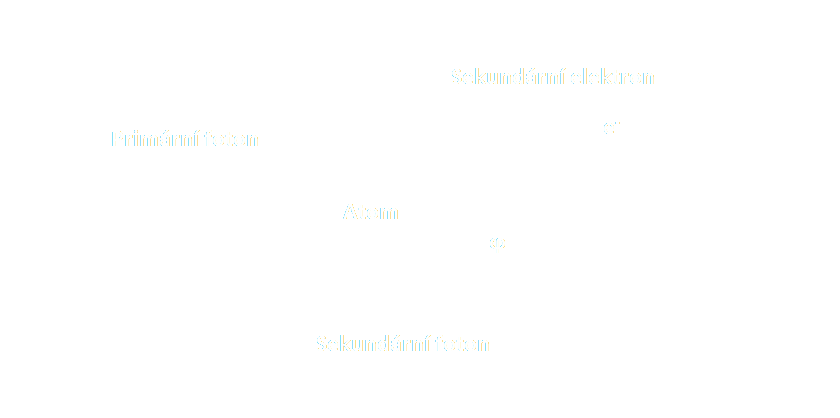
Comptonův jev

• Dokazuje, že záření má částicové vlastnosti
• Tento jev nastává při srážce elektronu (atomu) s fotonem
• Po strážce se mění vlnová délka záření

---

Vlnové vlastnosti částic

De Broglieho vlnová hypotéza - přišel s myšlenkou, že by i ostatní částice (elektrony, protony…) mohly mít některé vlnové vlastnosti. Každé pohybující se částici přiřadil jistou vlnu o vlnové délce:

$$\lambda = \frac{h}{p}$$

Klasická mechanika: jsme schopni určit polohu bodu v čase pokud známe jeho vektor rychlosti

Kvantová mechanika: jsme schopni určit hustotu pravděpodobnosti výskytu dané částice pomocí absoutní hodnoty druhé mocnici vlnové fukce $\lvert \Psi \rvert ^ 2$

---

Fotometrie

• zabývá se měřením a studiem záření

• Světelný tok - přenos světla prostorem - $\Phi$ [lm - lumen]
• Svítivost - vlastnost zdroje - $I$ [cd - candela]
• Osvětlení - účinky dopadu světla na povrch $E$ [lx - lux]

$$\begin{aligned} I &= \frac{\Delta \Phi}{\Delta \Omega} \\ E &= \frac{\Delta \Phi}{\Delta S} \\ E &= \frac{I}{r^2}\cos \alpha \end{aligned}$$

• $\Omega$ - prostorový úhel
• $S$ - plocha, na kterou dopadá světlo
• $r$ - vzdálenost plochy, na kterou dopadá světlo, od zdroje
• $\alpha$ - úhel mezi paprskem a kolmicí dopadu