PHYSICS

Základní principy speciální teorie relativity

[Edit]

Klasická mechanika

Speciální teorie relativity

1. Princip relativity

Žádným pokusem uvnitř vztažné soustavy nelze rozhodnout, jestli se pohybuje rovnoměrným pohybem, nebo je v klidu.

2. Princip stálé rychlosti světla

Ve všech vztažných soustavách má rychlost světla ve vakuu stejnou velikost cc a to maximální (c≈3.108c \approx 3.10^{8} m.s−1^{-1})

Tyto postuláty mají následující důsledky:

Relativnost času

Současnost dvou nesoumístných událostí je relativní pojem. Dvě nesoumístné události, které jsou současné k soustavě K’K’ nemusí být současné k soustavě KK →\rightarrow čas je relativní.

Dilatace času

Hodiny H’H’ pohybující se vzhledem k pozorovateli jdou pomaleji než hodiny HH, které jsou vzhledem k pozorovateli v klidu.

Odvození vzorce:

Máme dvě soustavy S′S' (kosmonaut, uvnitř rakety) a SS (pozorovatel, mimo raketu).

Pro kosmonauta platí, že paprsek ve světelných hodinách (dvě zrcadla Z1Z_1 a Z2Z_2, mezi kterými se periodicky odráží paprsek světla) opíše jednu periodu (jeden tik) za t’=2lct’ = \frac{2l}{c}.

Dilatace času

Pro pozorovatele mimo raketu platí, že zatímco je vyslán paprsek od jednoho zrcadla ke druhému, tak dojde k posunutí zrcadel o ∣AD∣=vΔt2\lvert AD \rvert = v\frac{\Delta t}{2} a paprsek urazí dráhu ∣AB∣=cΔt2\lvert AB \rvert = c\frac{\Delta t}{2}, kde Δt\Delta t je jedna perioda (jeden tik). Vzniká zde pravoúhlý trojúhelník, kde platí:

∣AB∣2=∣AD∣2+∣BD∣2\lvert AB \rvert ^{2} = \lvert AD \rvert ^{2} + \lvert BD \rvert^{2}

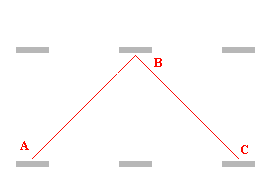
Dilatace času

Po dosazení do vzorce dostáváme:

(cΔt2)2=(vΔt2)2+l2\left (c\frac{\Delta t}{2} \right )^2 = \left (v\frac{\Delta t}{2} \right )^2 + l^2

Po uprávě vzorce:

Δt=2lc1−v2c2\Delta t = \frac{2l}{c\sqrt{1 - \frac{v^2}{c^2}}}

A po dosazení Δt′\Delta t' = 2lc\frac{2l}{c} dostáváme:

Δt=Δt′1−v2c2\Delta t = \frac{\Delta t'}{\sqrt{1 - \frac{v^2}{c^2}}}

Kontrakce délky

Pohybující tyč je vždy kratší než stejná tyč, vzhledem k níž jsme v klidu. U více rozměrných těles se vždy zkracuje ta délka, která je ve směru pohybu.

Platí:

l=l01−v2c2l = l_{0} \sqrt{ 1 - \frac{v^2}{c^2} }

Skládání rychlostí

u=u′+v1+u′vc2u = \frac{u'+v}{1+ \frac{u'v}{c^2}}

Relativistická hmotnost

Hmotnost každého tělesa tělesa se s rostoucí rychlostí zvyšuje. Pokud rychlost tělesa vv = cc, pak je jeho hmotnost nekonečná.

m=m01−v2c2m = \frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}

Relativistická hybnost

I při rychlostech blížících se rychlosti světla se mění hybnost

p=m0v1−v2c2p = \frac{m_{0}v}{\sqrt{1-\frac{v^{2}}{c^{2}}}}

Vztah mezi energií a hmotností

Při každé změně energie soustavy pohybující se rychlostí vv blížící se cc se změní i její hmotnost čím dál pozorovatelněji.

ΔE=Δmc2\Delta E = \Delta mc^2

Využití