PHYSICS

Kmitání

May 23 2020 [Edit]

• Mechanické kmitání
  • Mechanický oscilátor
  • Harmonické kmitání
  • Fáze kmitavého pohybu
  • Složené kmitání
  • Dynamika kmitavého pohybu
  • Kyvadlo
  • Energie v mechanickém oscilátoru
  • Nucené kmitání
  • Rezonance
• Elektromagnetické kmitání
  • Thomsonův vztah
  • Napětí
  • Proud
  • Nucené kmitání elektromagnetického oscilátoru

---

Mechanické kmitání

Mechanický oscilátor

Zařízení, které kmitá bez vnějšího působení

• Závaží na pružině, kyvadlo, bod na kole.
• Trajektorie kmitání je různá

Když zavěsíme těleso na pružinu, tak se mechanický oscilátor zastaví v rovnovážné poloze. Zde na něj působí dvě síly, gravitační $\vec F_{g}$ a síla pružnosti $\vec F_{p}$, která má opačný směr.

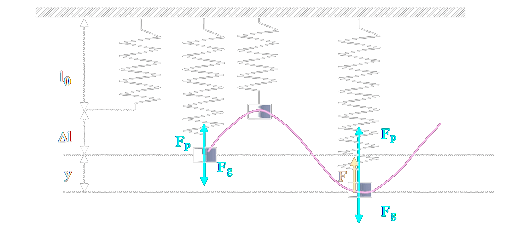
Časový diagram

• Dráha, kterou urazí za určitý čas, se mění – nerovnoměrný pohyb
• Jedná se o periodický děj, tedy po uplynutí určité doby se dostane oscilátor do stejné polohy
• Tuto periodicky opakující se část nazýváme kmit
• Kmity nám charakterizují dvě veličiny:

$$f = \frac{1}{T}$$

• $T$ - Perioda [s] - jak dlouho trvá jeden kmit
• $f$ - Frekvence [Hz] - počet kmitů za jednu sekundu

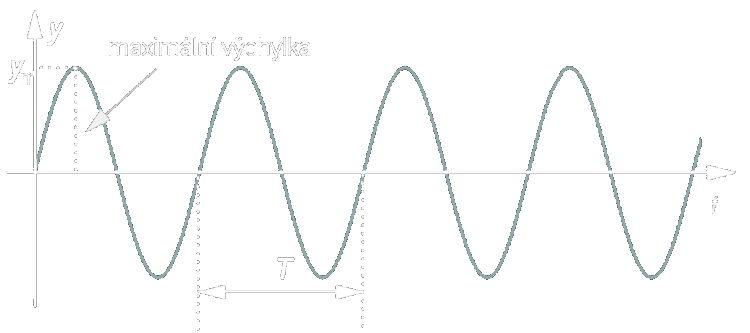
Harmonické kmitání

• Jestliže mechanický oscilátor kmitá, je okamžitá poloha těžiště tělesa určena souřadnicí $y$ - okamžitá výchylka
• $y_{m}$ - Absolutní hodnota největší výchylky neboli amplituda výchylky
• Každý bod zvolený na oscilátoru se bude pohybovat úhlovou rychlostí $\omega = \frac{2\pi}{T} = 2\pi f$

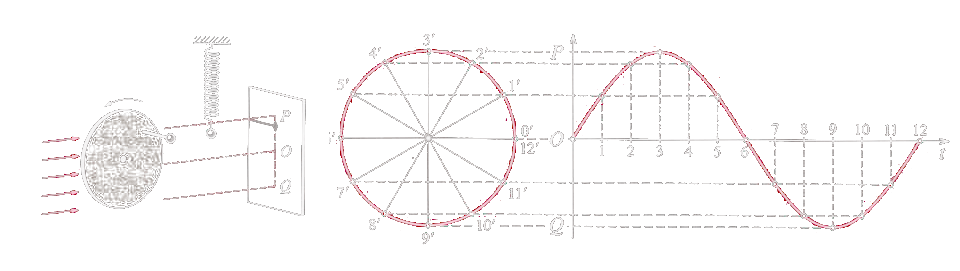
Pokud kruhový děj započneme v bodě kde $y = 0$ pak:

$$y = y_{m}\sin(\omega t)$$

Rychlost:

$$v = v_{0}\cos(\omega t) = \omega y_{m}\cos(\omega t)$$ $$\downarrow$$ $$v_{m} = \omega y_{m}$$

Zrychlení:

$$a = -a_{0}\sin(\omega t) = \omega^{2}y_{m}\sin(\omega t) = -\omega^{2}y$$ $$\downarrow$$ $$a_{m} = \omega^{2}y$$

Fáze kmitavého pohybu

Kmitání, které jsme si doposud ukázaly, začínalo v počáteční poloze kdy $y = 0$. Ale takto se vyskytuje velmi málo. Rovnice pro harmonické kmitání bude vypadat:

$$y = y_{m}\sin \left( \omega \left[t+t_{0} \right]\right) = y_{m}\sin(\omega t+\varphi_{0})$$

• $\varphi_{0}$ - Počáteční fáze kmitavého pohybu.

Složené kmitání

• Vzniká, když spojíme dohromady dvě kmitání
• Rázy - Vznikají v případě, kdy se amplituda výchylky výsledného kmitání periodicky zvětšuje a zmenšuje

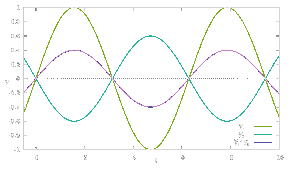
Jestliže hmotný bod koná současně více harmonických kmitavých pohybů téhož směru s okamžitými výchylkami $y_{1}, y_{2} ... y_{k}$, je okamžitá výchylka $y$ výsledného kmitání (okamžité výchylky mohou být i opačné ale pak se mění znaménko na záporné):

$$y_{1}+y_{2}+ .... +y_{k} = y$$

Dynamika kmitavého pohybu

$$F = - m\omega^{2}y$$

Parametry oscilátoru ovlivňuje hmotnost závaží a tuhost pružiny $k$:

• $k = \frac{F}{\Delta l}$ $$
• $\Delta l$ - délka pružiny před a po pověšení závaží

Pokud je hmotný bod (závaží) v rovnovážné poloze platí, že $F_{g} = F_{p}$ pak tedy:

$$k\Delta l = mg$$

A pokud těleso vychýlíme z rovnovážné polohy pak $F = F_{p}+F_{g}$ z čehož po vyjádření:

$$-ky = m\omega^{2}y$$ $$\omega = \sqrt{\frac{k}{m}}$$

• $T = 2\pi\sqrt{\frac{m}{k}}$ $$
• $f = \frac{1}{2\pi}.\sqrt{\frac{k}{m}}$ $$

Kyvadlo

Příčinou kmitavého pohybu kyvadla je pohybová složka $F$ a tíhové síly $F_{g}$, která vzniká při vychýlení kyvadla z rovnovážné polohy.

Platí:

$$\begin{aligned} \sin\alpha &= \frac{F}{F_{g}} = \frac{y’}{l} \\ F &= \frac{F_{g}}{l}.y \\ T &= 2\pi\sqrt{\frac{m}{k}} \end{aligned}$$

Energie v mechanickém oscilátoru

• Pro periodický děj oscilátoru je charakteristické, že mění energii
• V oscilátorech jsou dvě typické potenciální energie
  • Potenciální energie tíhová - $E_{pt}$
  • Potenciální energie pružnosti- $E_{pr}$

$$\begin{aligned} E_{pr} &= \frac{1}{2}k(\Delta l)^2 \\ E_{pt} &= mgh \\ E &= mgh + \frac{1}{2}k\Delta l^2 + \frac{1}{2}k.y^2 + \frac{1}{2}m.v^2 \end{aligned}$$

Nucené kmitání

Vzniká působením periodické síly na oscilátory i na objekty, které vlastnosti oscilátoru nemají. Frekvence nuceného kmitání závisí na frekvenci působící síly a nezávisí na vlastnostech kmitajícího objektu.

Rezonance

Význam rezonance spočívá v tom, že umožňuje rezonanční zesílení kmitů. Malou, periodicky působící silou lze v oscilátoru vzbudit kmitání o značné amplitudě výchylky, pokud je perioda vnější působení shodná s periodou vlastního kmitání osciláru.

Elektromagnetické kmitání

Zdrojem elektromagnetického kmitání je oscilátor, v něm se periodicky mění elektrické pole na magnetické a z magnetického na elektrické

• $L$ - indukčnost cívky
• $C$ - kapacita kondenzátoru

Nejjednodušší oscilátorem je spojení cívky a kondenzátoru, neboli LC obvod

Napětí na kondenzátoru:

$$U_{c} = X_{c}.I$$

Napětí na cívce:

$$U_{L} = X_{L}.I$$

Thomsonův vztah

Thomsonův vztah určuje periodu vlastního kmitání

$$T = 2\pi\sqrt{2}{LC}$$ $$f = \frac{1}{2\pi\sqrt{LC}}$$

Napětí

$$U = U_{m}cos(\omega_{0}t)$$

Proud

Indukovaný proud je opožděn o čtvrtinu periody neboli o polovinu $\pi$

$$I = I_{m}cos(\omega.t-\frac{\pi}{2})$$

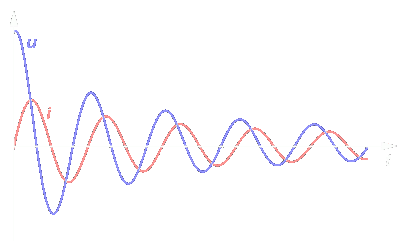
Předchozí vztahy platí především pro ideální případ, kdy je odpor zanedbatelný a kmitání harmonické

Nucené kmitání elektromagnetického oscilátoru

Netlumené kmitání vzniká tehdy, když jsou ztráty po utlumení nahrazeny v průběhu celé periody. Například připojením ke zdroji harmonického napětí. V oscilačním obvodu pak kmitá harmonicky s úhlovou frekvencí, která se může lišit od úhlové frekvence vlastního úhlového kmitání. Tak vznikne nucené kmitání.

Rezonance - Vytváří se, když se vlastní kmitání shodne s nuceným kmitáním