PHYSICS

Struktura a vlastnosti pevných látek

May 21 2020 [Edit]

• Úvod
• Krystalické látky
  • Ideální krystalová mřížka
    • Druhy základních kubických buněk
  • Poruchy krystalové mřížky
• Amorfní látky
• Vazby v pevných látkách
• Deformace pevného tělesa
  • Druhy deformací
  • Základní deformace
    • Deformace tahem
    • Deformace tlakem
    • Deformace ohybem
    • Deformace smykem
    • Deformace kroucením
• Síla pružnosti $F_p$
  • Normálové napětí $\sigma_n$
  • Křivka deformace
  • Hookův zákon pro pružnou deformaci tahem
• Teplotní roztažnost pevných látek
  • Teplotní délková roztažnost
  • Teplotní objemová roztažnost
• Změna skupenství
  • Tání
  • Tuhnutí (krystalizace)
  • Sublimace
  • Desublimace

---

Úvod

Pevné látky jsou látky, které si zachovávají svůj tvar = odlišnost od kapalných a plynných látek. Dělí se na krystalické a morfní.

---

Krystalické látky

• Pravidelné uspořádání částic (atomů, molekul, iontů); vyskytují se buď jako monokrystaly nebo polykrystaly
• Monokrystaly – pravidelné uspořádání částic uvnitř monokrystalu
  • dalekodosahové uspořádání
  • Jsou anizotropní - vlastnosti závislé na směru vzhledem ke stavbě krystalu
  • Například NaCl, SiO$_2$, diamant,…
• Polykrystaly
  • většina pevných látek (všechny kovy, zeminy, prach,…), skládají se z velkého počtu drobných krystalů – zrn (10μm - několik milimetrů)
  • uvnitř zrn jsou částice uspořádány pravidelně, poloha zrn je však náhodná struktura monokrystalu struktura polykrystalu
  • Jsou izotropní - vlastnosti jsou ve všem směrech stejné (roztažnost při zahřívání)

Struktura monokrystalu	Struktura polykrystalu	Krystalická forma SiO$_2$

Ideální krystalová mřížka

• Je hmotný útvar, který vznikne, když je prostorová pravoúhlá geometrická mřížka obsazena pravidelně rozloženými částicemi
• Obsahuje základní (elementární) buňku = základní krychle obsazená určitým způsobem částicemi, patří do krychlové soustavy → posouváním této základní krychle podél jejích prodloužených hran vzniká ideální krystalická mřížka

• $a$ - mřížkový parametr (mřížková konstanta) = Délka hrany základní buňky

Druhy základních kubických buněk

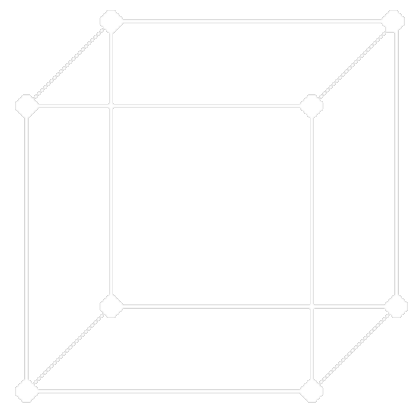
• Prostá
  • Na jednu základní buňku připadá $8 × \frac{1}{8}$ = 1 atom.
  • Každý vrchol buňky je společný osmi buňkám.
  • Například Polonium alfa
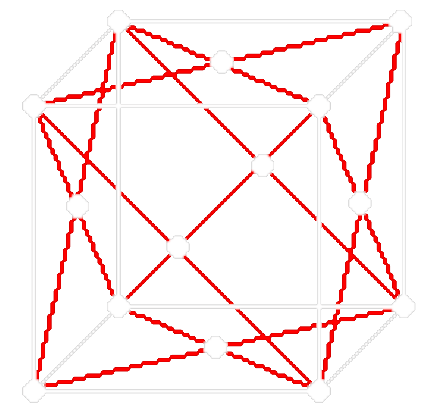
• Plošně centrovaná
  • Na jednu základní buňku připadá $8 × \frac{1}{8} + 6 × \frac{1}{2}$ = 4 atomy
  • Každý vrchol buňky je společný osmi buňkám, každá stěna dvěma buňkám
  • Například Al, Cu, Ni, Au
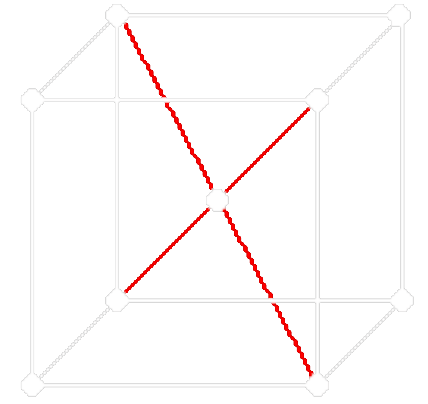
• Prostorově centrovaná
  • Na jednu základní buňku připadá $8 × \frac{1}{8} + 1$ = 2 atomy
  • Každý vrchol buňky je společný osmi buňkám, „prostřední“ atom náleží pouze k dané buňce
  • Například Li, Na, K, Cr, Si, diamant

Prostá buňka	Plošně centrovaná buňka	Prostorově centrovaná buňka

Poruchy krystalové mřížky

Vyskytují u všech krystalů – každý reálný krystal má poruchy (defekty) – nejjednodušší jsou bodové poruchy

• Vakance
  • z latiny: volné místo
  • porucha vzniklá neobsazením rovnovážné polohy částice v krystalové mřížce
  • příčina: tepelný kmitavý pohyb částic, ozáření krystalu
• Intersticiální poloha částice
  • z latiny uložený v mezeře
  • částice je v místě mimo pravidelný bod krystalové mřížky
  • souvisí s vakancí
• Příměsi (nečistoty)
  • cizí částice, které se vyskytují v krystalu daného chemického složení
  • tato částice se může nacházet buď v intersticiální poloze (absorpce H$_2$, C, O2, N$_2$ v kovech) nebo nahrazuje vlastní částici mřížky (P vpraven do Si – vznik příměsového polovodiče)

Vakance	Intersticiální poloha částice	Příměsi

---

Amorfní látky

• Periodické uspořádání částic je omezeno na vzdálenost do zhruba 10$^{-8}$ m, na větších vzdálenostech je pravidelnost uspořádání porušena. Amorfní látky se vyznačují krátkodosahovým uspořádáním.
• Patří sem sklo, pryskyřice, vosk, asfalt, plasty a další.
• Polymery
  • Tvoří zvláštní skupinu amorfních látek organického původu
  • Například kaučuk, bavlna, celulóza, bílkoviny, PVC
  • Jejich dlouhé makromolekuly jsou často navzájem propleteny, stočeny do klubíček nebo vytvářejí sítě.

Amorfní forma SiO$_2$

---

Vazby v pevných látkách

Vazebné síly působí vždy, váží k sobě částice, z nichž se látka (krystalová mřížka) skládá - u pevných látek se jedná o tyto vazby:

• Iontová vazba - alkalické halogenidy (NaCl, KBr, CsCl), oxidy alkalických zemin (CaO)
  • jedná se o vazbu mezi elektronegativním a elektropozitivním prvkem
  • vazba se uskutečňuje pomocí elektronu (kationt a aniont) – přitahují se elektrostatickou silou
  • iontové krystaly jsou tvrdé, mají vysokou teplotu tání, jsou křehké a štěpné podél rovin kolmých na hrany základní buňky, za běžných teplot - elektrické izolanty, při vyšších teplotách - vodivé, propustné pro viditelné světlo
• Vodíkový můstek
  • spojuje např. krystaly ledu vody
  • často se vyskytuje v organických látkách
  • krystaly jsou křehké
  • mají nízkou tepelnou vodivost
  • plavou na vodě
• Kovová vazba
  • atomy kovových prvků (např. Cu, Fe, Al,…)
  • mají maximálně tři valenční elektrony (slabě vázané k atomovému jádru – snadné uvolnění) $\rightarrow$ volné elektrony vytvářejí tzv. elektronový plyn
  • kovové krystaly mají velmi dobrou tepelnou a elektrickou vodivost, povrchový lesk a v silnějších vrstvách jsou neprůhledné.
  • Nejsou štěpné a některé se vyznačují dobrou kujností a tažností.
• Kovalentní vazba
  • podstatou vazby je tzv. sdílení elektronů sousedními atomy
  • tato vazba je směrová (uskutečňuje se pouze pod určitými úhly) a nasycená (je nasycená mocenstvím vázaných atomů)
  • v přírodě je velmi rozšířená - atomy nekovových prvků se váží samy se sebou v molekuly (H$_2$ , Cl$_2$ , O$_2$, CH$_4$, H$_2$O, HNO$_3$)
  • kovalentní (atomové) krystaly jsou tvrdé, mají vysokou teplotu tání, jsou nerozpustné v běžných rozpouštědlech a patří mezi elektrické izolanty nebo polovodiče
• Van der Waalsovy síly – krystaly inertních plynů (H$_2$ , Cl$_2$ , O$_2$), organické sloučeniny (parafín)
  • jde o slabou vazbu (vazba elektrické povahy)
  • mají nízkou teplotu tání a jsou měkké

---

Deformace pevného tělesa

Deformace tělesa je změna rozměrů, tvaru nebo objemu tělesa, která je způsobena vnějšími sílami.

Druhy deformací

• Pružná (elastická) – Když přestanou působit vnější síly, deformace vymizí
  • V praxi malé prodloužení pružiny, ohnutí ocelového pásku, …
• Tvárná (plastická)
  • Deformace, která přetrvává i pokud přestanou působit vnějšími síly
  • Například změna tvaru kovového tělesa při kování nebo válcování, …
  • V praxi se vyskytují většinou oba druhy deformace současně.

Základní deformace

V praxi se daleko častěji opět vyskytují deformace složené z několika jednoduchých deformací. Při deformaci jsou částice působením vnějších sil vychylovány ze svých rovnovážných poloh. Tomu brání síly vzájemného působení mezi částicemi pevného tělesa. Při deformaci tak vznikají v tělese síly pružnosti.

Deformace tahem

Na těleso působí dvě stejně velké síly ve směru ven z tělesa, které leží na téže vektorové přímce. Tato vektorová přímka u pravidelných těles většinou splývá s osou souměrnosti. Například zavěšené lano jeřábu, výtahu,…

Deformace tlakem

Od deformace tahem se liší pouze tím, že působící síly míří dovnitř tělesa. Například pilíře mostu, nosníky konstrukce domů, …

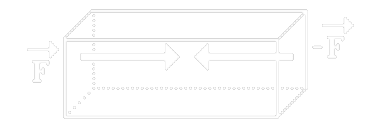
Deformace ohybem

U těles, na něž působí síla kolmo k jejich podélné ose. Dolní vrstvy tělesa jsou deformovány tahem, horní vrstvy tlakem a střední vrstva zachovává svou délku. Např. tyč podepřená na obou koncích, …

Deformace smykem

Na horní a dolní podstavu těles působí tečné opačně orientované síly v rovinách těchto podstav. Síly způsobují vzájemné posunutí jednotlivých vrstev tělesa, přičemž se nemění jejich vzdálenost. Např. šroub, nýt,…

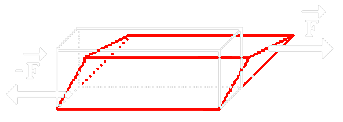
Deformace kroucením

Je způsobena dvěma silovými dvojicemi, jejichž momenty jsou stejné velké, ale mají opačný směr. Např. hřídele strojů, vrtáky při vrtání, šrouby během utahování, …

---

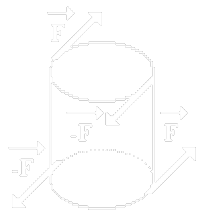
Síla pružnosti $F_p$

Je-li těleso pružně deformováno tahem nebo tlakem, je v rovnovážném stavu velikost síly pružnosti $\vec F_p$ rovna velikosti deformující síly $\vec F$.

Normálové napětí $\sigma_n$

Vzniká v příčném řezu deformovaného tělesa (stav napjatosti)

$$\sigma_n = \frac{F_p}{S}$$

• $\sigma_n$ - normálové napětí [Pa]
• $F_p$ - síla pružnosti
• $S$ - plocha řezu kolmého k vektoru síly $\vec F_p$

Křivka deformace

Graf závislosti normálového napětí na relativním prodloužení

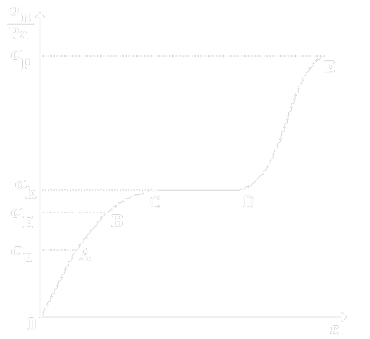
• $0A$ - průžná deformace (když přestaneme působit silou, těleso se vrátí do původního stavu) $\rightarrow$ platí Hookův zákon
• $\sigma_u$ - mez úměrnosti
• $AB$ - oblast dopružování
• $\sigma_E$ - mez pružnosti - největší hodnota normálového napětí, kdy je deformace ještě pružná. Po překročení je těleso trvale deformováno.
• $CD$ - tečení materiálů (tažení drátu)
• $\sigma_k$ - mez kluzu
• $DE$ - zpevnění materiálu
• $\sigma_p$ - mez pevnosti - po překročení této hodnoty normálového napětí dojde k porušení materiálu - přetrhne se, rozdrtí se
• dovolené napětí - nejvyšší přípustná hodnota $\sigma_n$ při deformaci tahem nebo tlakem. Jeho hodnota je značně menší než mez pevnosti. Podíl meze pevnosti a dovoleného napětí je koeficient bezpečnosti

Hookův zákon pro pružnou deformaci tahem

Při dehormaci tahem se těleso prodlužuje

$$\Delta l = l - l_0$$

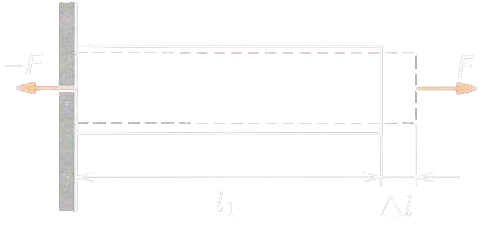
• $l$ - aktuální délka
• $l_0$ - původní délka

Relativní prodloužení $\epsilon$

$$\epsilon = \frac{\Delta l}{l_0}$$

Při pružné deformaci tahem je normálové napětí přímo úměrné relativnímu prodloužení.

$$\sigma_n = E\epsilon$$ $$\Delta l = \frac{F_pL_1}{ES}$$

• $E$ - modul pružnosti v tahu [Pa] (v MFChT)

---

Teplotní roztažnost pevných látek

Fyzikální jev spočívající ve změně rozměrů tělesa při změně jeho teploty

Teplotní délková roztažnost

Prodloužení tyče je přímo úměrné počáteční délce tyče a přírůstku její teploty. (když se změní teplota, změní se i délka)

$$\Delta l = \alpha l_0 \Delta t$$ $$l = l_0 [1 + \alpha (t - t_0)]$$

• $\alpha$ - teplotní součinitel délkové roztažnosti [K$^{-1}$] (v MFChT)
• $t$ - teplota tělesa

Teplotní objemová roztažnost

Při změně teploty se změní i objem

$$V = V_0[1 \beta (t - t_0)]$$

• $\beta$ - teplotní součinitel roztažnosti [K$^{-1}$], $\beta \approx 3\alpha$

---

Změna skupenství

Tání

• Přechod pevného skupenství do kapalného
• Teplota tání - teplota, při které začíná krystalická látka tát
• měrné skupenské teplo tání $l_t$

$$l_t = \frac{L_t}{m}$$

• $L_t$ - skupenské teplo tání [J.kg$^{-1}$]

Tuhnutí (krystalizace)

• Přechod látky ze skupenství kapalného ve skupenství pevné
• Krystalizace = děj, při kterém vzniká krystalická látka, teplota krystalizace (rovna teplotě tání)
• Po dosažení krystalizační teploty vznikají krystalizační jádra (zárodky). Postupně vytvářejí zrna (vznik polykrystalické látky
• Vytvoří-li se pouze jeden zárodek = vznik monokrystalu

Sublimace

• Přeměna látky z pevného skupenství přímo na skupenství plynné (led, sníh, jod)
• Pro měrné skupenské teplo sublimace $l_s$

$$l_s = \frac{L_s}{m}$$

• $L_s$ - skupenské teplo sublimace

Desublimace

• přeměna látky ze skupenství plynného přímo ve skupenství pevné (jinovatka)