MATHEMATICS

Propositional logic

April 29 2020 [Edit]
[EN/CZ]

Annotation

Operation	Notation	Sentece representaion
Negation	$\neg$A ; A’	not A
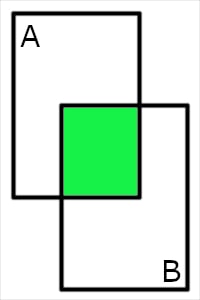
Conjuncion	A $\land$ B	A and B
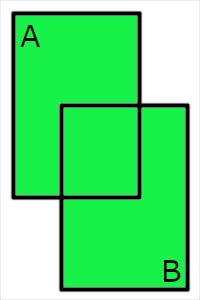
Disjunction	A $\lor$ B	A or B
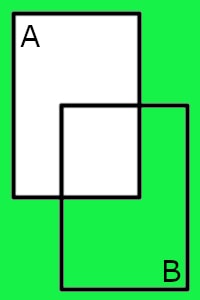
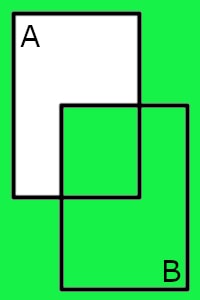
Implication	A $\implies$ B	Impossible A without B
Equivalence	A $\iff$ B	If A, then B

Table of values

A	B	$\neg$A	A $\land$ B	A $\lor$ B	A $\Rightarrow$ B	A $\Leftrightarrow$ B
1	1	0	1	1	1	1
1	0	0	0	1	0	0
0	1	1	0	1	1	0
0	0	1	0	0	1	1

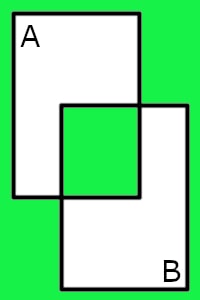Negation

Expression	Negation of expression
A $\land$ B	$\neg$A $\lor$ $\neg$B
A $\lor$ B	$\neg$A $\land$ $\neg$B
A $\iff$ B	(A $\lor$ B) $\land$ ($\neg$A $\lor$ $\neg$B)
A $\implies$ B	A $\land$ $\neg$B