PHYSICS

Molekulová fyzika a termika

May 08 2020 [Edit]

• Hmota
  • Plynné látky
    • Ideální plyn
    • Rychlost molekul plynu
      • Střední kvadratická rychlost molekul
      • Střední kinetická energie
    • Tlak ideálního plynu
    • Změna vnitřní energie
    • První termodynamický zákon
    • Stavové veličiny
      • Stavová rovnice plynu
    • Izolované soustavy
  • Kapalné látky
  • Pevné látky
    • Krystalická struktura pevných látek
      • Ideální krystalická mřížka
    • Amorfní struktura pevných látek
• Brownův pohyb
• Silové působení částic
• Přenos vnitřní energie
  • Tepelná výměna vedením
  • Tepelná výměna zářením
  • Tepelná výměna prouděním
• Měrná tepelná kapacita
• Tepelná kapacita
  • Kalorimetrická rovnice

---

Hmota

• Hmota je složena z částic. Ty na sebe působí přitažlivými i odpudivými silami. Zároveň také vykonávají tepelný pohyb (Brownův pohyb).
• Částice v látkách se neustále neuspořádaně pohybují
• Všechny směry částic jsou stejně pravděpodobné u tělesa v klidu
• Tepelný pohyb = neustálý neuspořádaný pohyb částic
• Difuze - samovolné pronikání částic jedné látky mezi částice druhé látky
• Tlak plynu - narážení molekul plynu na okolní tělesa

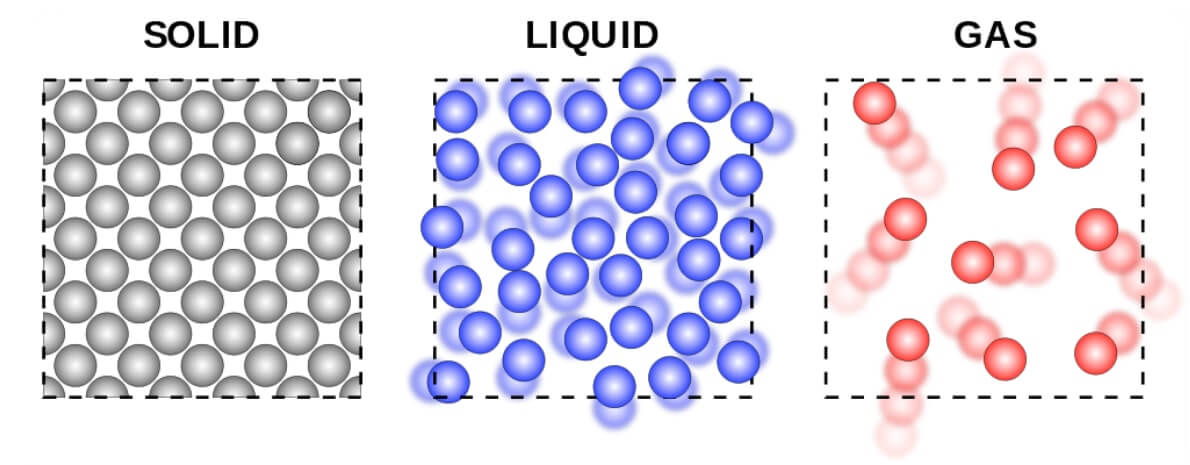
Plynné látky

• tepelný pohyb - různé směry, různé rychlosti
• všechny směry jsou stejně pravděpodobné
• vyšší teplota = vyšší rychlost molekul
• velké vzdálenosti mezi molekulami (3 nm)
• převládá posuvný pohyb (rotační + vibrační)
• hodnota potenciální energie je ve srovnání s kinetickou zanedbatelná

Ideální plyn

Splňuje 3 následující atributy:

1. Rozměry molekul ideálního plynu jsou ve srovnání se střední vzdáleností molekul od sebe zanedbatelně malé
2. Molekuly ideálního plynu mimo vzájemné
3. Vzájemné srážky molekul ideálního plynu a srážky těchto molekul se stěnou nádoby jsou dokonale pružné

V normálních podmínkách je možné většinu plynů považovat za ideální

Rychlost molekul plynu

Molekuly plynu, který je v rovnovážném stavu, nemají v určitém okamžiku stejnou rychlost. Rozdělení molekul ideálního plynu tabulkou nebo grafem.

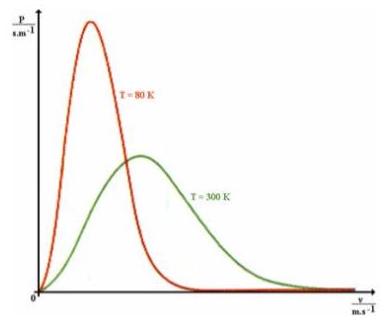
Střední kvadratická rychlost molekul

Definujeme jako rychlost posuvného pohybu molekul, kterou by musely mít všechny molekuly plynu, aby jejich celková kinetická energie byla rovna skutečné kinetické energii molekul. Střední kvadratická rychlost je určena vztahem:

$$v_k^2 = \frac{\sum_{i = 1}^m N_iv_i^2}{N}$$

Druhá mocnina střední kvadratické rychlosti je tedy rovna součtu druhých mocnin rychlostí všech molekul, dělených počtem molekul. Tato rychlost závisí na termodynamické teplotě podle vztahu:

$$v_k = \sqrt{\frac{3kT}{M_0}}$$

• $k$ = $1,38 . 10^{-23} J.K^{-1}$ - Boltzmannova konstanta

Střední kinetická energie

je energie, kterou má molekula v důsledku neuspořádaného posuvného pohybu

$$E_0 = \frac{1}{2}m_0v_k^2 = \frac{3}{2}kT$$

Tlak ideálního plynu

$$p = \frac{1}{3}N_vm_0v_k^2$$

Změna vnitřní energie

• Vnitřní energie tělesa lze měnit dějem, který nazýváme konání práce.
• Při dějích probíhajících v izolované soustavě těles zůstává součet kinetické, potenciální a vnitřní energie těles konstantní
• Změna vnitřní energie při tepelné výměně
  • Děj, při němž neuspořádaně se pohybující částice teplejšího tělesa narážejí na částice dotýkají se studenějšího tělesa a předávají jim část své energie, nazýváme tepelná výměna
  • Teplo $Q$ je určeno energií, kterou při tepelné výměně odevzdává teplejší těleso studenějšímu. Jednotkou tepla je Joule [J]

První termodynamický zákon

Přírůstek vnitřní energie $\Delta U$ soustavy se rovná součtu práce $W$ vykonané okolními tělesy působící na soustavu silami a tepla $Q$ odevzdaného okolními tělesy soustavě:

$$\Delta U = W + Q$$

Stavové veličiny

1. Tlak
2. Teplota
3. Objem

Každá soustava se snaží dojít do rovnovážného stavu.

Stavová rovnice plynu

$$pV = nRT$$

• $p$ = tlak
• $V$ = objem
• $n$ = látkové množství plynu
• $R$ = molární plynová konstanta
• $T$ = termodynamická teplota plynu

Izolované soustavy

• Isotermický děj
  • Teplota je konstantní
  • $pV = konst$ $$
• Isochorický děj
  • Objem se nemění
  • $\frac{p}{T} = konst$ $$
• Isobarický děj
  • Tlak se nemění
  • $\frac{V}{T} = konst$ $$
• Adiabatický děj
  • soustava si nepředává žádné teplo s okolím
  • $Q = 0$ $$

Kapalné látky

• vzdálenost mezi částicemi je 0,2 nm
• molekuly nejsou vázány do stejné rovnovážné polohy - časem se mění
• působení vnějších sil - tekutina se pohybuje ve směru sil
• potenciální a kinetická energie se od sebe velikostně příliš neliší

Pevné látky

• struktura je krystalická nebo amorfní
• vzdálenost mezi částicemi je 0,2 až 0,3 nm
• přitažlivé síly způsobují určitý tvar a objem pevné látky
• působí-li vnější síly nebo se nemění teplota - tvar i objem se nemění
• vibrační chaotický pohyb v mřížce - s teplotou se výchylky zvětšují
• potenciální energie soustavy je mnohem větší než kinetická energie částic

Struktura pevných látek

Krystalická	Amorfní

Krystalická struktura pevných látek

• všechny částice jsou v jedné krystalické struktuře, která není přerušená, rozložení částic se periodicky opakuje v celém krystalu.
• Celý monokrystal má pravidelný geometrický tvar.
• Vlastnosti monokrystalů se v určitých směrech mohou lišit – jsou závislé na jejich uspořádání (slída se v jednom směru snadno rozdělí na plátky, ale tyto plátky je velmi obtížné rozdělit)
• Monokrystaly
  • Všechny částice jsou v jedné krystalické struktuře, která není přerušená, rozložení částic se periodicky opakuje v celém krystalu.
  • Celý monokrystal má pravidelný geometrický tvar.
  • Vlastnosti monokrystalů se v určitých směrech mohou lišit – jsou závislé na jejich uspořádání (slída se v jednom směru snadno rozdělí na plátky, ale tyto plátky je velmi obtížné rozdělit)
• Polykrystaly
  • Skládají se z velkého počtu drobných krystalků, zrn (rozměry od 10 mm po několik mm)
  • Částice uvnitř mají opakující se strukturu, ale zrna jsou uspořádány nahodile
  • Mají ve všech směrech stejné vlastnosti. Patří sem všechny kovy

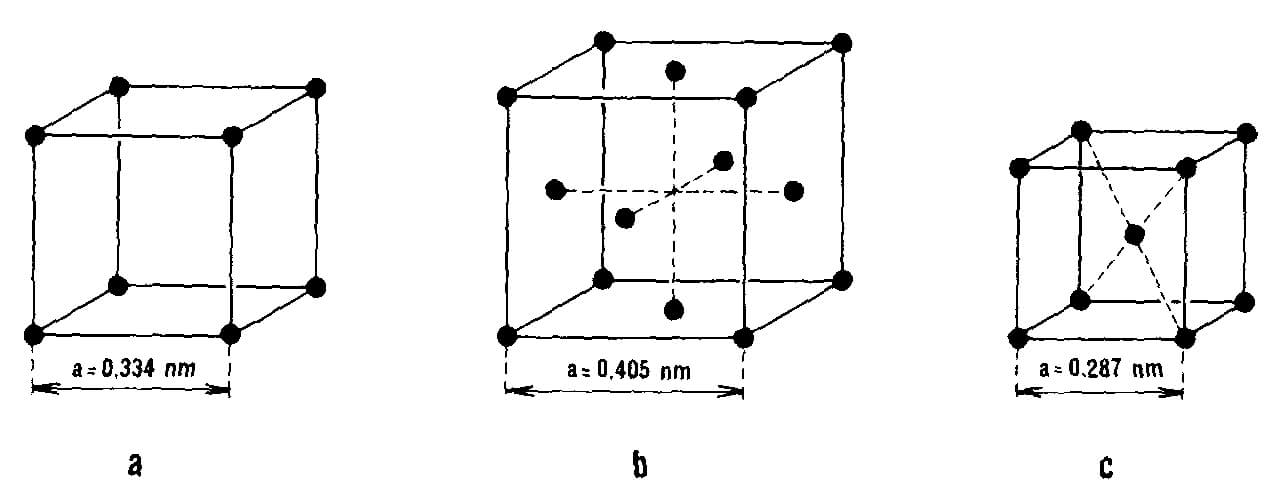
Ideální krystalická mřížka

• Základem je elementární buňka, která je vždy rovnoběžnostěn.
  • Kubická základní buňka může být prostá (primitivní)
  • Plošně centrovaná – vrcholy krychle a středy stěn (14 bodů)
  • Prostorově centrovaná – vrcholy krychle a střed krychle (9 bodů)
• Délka hrany základní buňky je mřížkový parametr a (nebo mřížková konstanta).
• Částice v krystalu kmitají kolem bodů krystalové mřížky.

Amorfní struktura pevných látek

• Periodické uspořádání těchto částic je velmi omezeno
• Pro větší vzdálenosti je struktura látky porušena. Struktura amorfních látek má krátkodosahové uspořádání.
• Patří sem sklo, pryskyřice, vosk, asfalt, mnohé plasty.

Brownův pohyb

• Díky tepelnému (Brownově pohybu) se odehrávají děje jako difuze a osmóza. Taky má na svědomí tlak plynu.
• Částice se pohybují chaoticky všemi směry a různými rychlostmi. S rostoucí teplotou roste i rychlost částic.

Silové působení částic

Částice na sebe navzájem působí silami. Tyto síly jsou při malých vzdálenostech odpudivé a při větších vzdálenostech přitažlivé

Přenos vnitřní energie

Přenos vnitřní energie z míst s vyšší teplotou do míst s nižší teplotou může uskutečnit vedením nebo zářením. Vnitřní energii může přenášet take proudící tekutina, v tom případě mluvíme o proudění

Tepelná výměna vedením

• Probíhá uvnitř tělesa
• Tepelná energie přechází z míst z míst s vyšší teplotou do studenějších
• V izolantech: částice v zahřívaném místě se rozkmitají a tím rozkmitají i částice ve svém okolí
• Ve vodičích: Tepelná výměna je hlavně zprostředkována volnými elektrony
• Různé materiály mají různou tepelnou vodivost
• Voda je velmi špatný tepelný vodič
• Plyny mají nejmenší tepelnou vodivost (duté cihly, textil, pěna)

Tepelná výměna zářením

• Spočívá v vyzařování a přijímání elektromagnetického záření
• Vzniká pohybem uvnitř atomů a molekul
• Při vyzáření energie, látka ztratí energii rovnající se energii záření
• Při dopadu na těleso se záření z části:
  • Odrazí
  • Projde
  • Pohltí
• Infra zářiče - zdroje tepelného záření
• Ohřívání země sluncem

Tepelná výměna prouděním

• Vzniká zahříváním kapaliny nebo plynu v tíhovém poli
• Chladnější kapalina má větší hustotu než teplejší
• Při zahřívání kapaliny zespodu, ohřátá kapalina proudí nahoru a chladná dolů (Vaření vody v hrnci, rychlovarná konvice, gejzíry)
• Pro zrychlení procesu se používá tzv. nucené proudění (chladič v autě, ventilátory, klimatizace)

Měrná tepelná kapacita

• značí se $C$
• jednotka je $J.KG^{-1}.K^{-1}$
• Jedná se o množství energie kterou musíme dodat tělesu aby se jeho teplota zvýšila o 1 stupeň Celsia/Kelvina
• platí:

$$C = Q/\Delta t$$

Tepelná kapacita

• značí se $c$
• jednotka je $J.K^{-1}$
• Jedná se o množství energie kterou musíme dodat jednomu kilogramu dané látky aby se jeho teplota zvýšila o 1 stupeň Celsia/Kelvina
• platí:

$$c = \frac{C}{m} = \frac{C}{m \Delta t}$$

Kalorimetrická rovnice

$$\begin{aligned} Q_1 &= Q_2 \\ c_1m_1(t-t_1) &= c_2m_2(t_2-t) \\ m_kc_k(t -t_1) + c_1m_1(t-t_1)&= c_2m_2(t_2-t) \end{aligned}$$

• $m_1$ = hmotnost kapaliny
• $c_1$ = měrná tepelná kapacita kapaliny
• $t_1$ = počáteční teplota vody

• $t$ = výsledná teplota

• $m_k$ = hmotnost kalorimetru

• $c_k$ = měrná tepelná kapacita kalorimetru

• $m_2$ = hmotnost tělesa
• $c_2$ = měrná tepelná kapacita tělesa
• $t_2$ = počáteční teplota tělesa
• $t$ = výsledná teplota