PHYSICS

Mechanika tuhého tělesa

May 08 2020 [Edit]

• Tuhé těleso a jeho pohyb
  • Pohyb tuhého tělesa:
• Moment síly
  • Momentová věta
  • Směr momentu sil
• Těžiště tuhého tělesa
  • Určení polohy tělesa
  • Podmínky rovnovážné polohy tuhého tělesa
• Rovnovážné polohy tuhých těles
• Kinetická energie tuhého tělesa
• Moment setrvačnosti tuhého tělesa vzhledem k ose otáčení

---

Tuhé těleso a jeho pohyb

• Tuhé těleso (dokonale tuhé těleso) je pro danou úlohu těleso, jehož tvar ani objem se v této úloze účinkem působících sil nemění.
• Síly, které na těleso působí, mají tedy pouze pohybové účinky.

Pohyb tuhého tělesa:

• Posuvný (translace) - všechny body tělesa konají pohyb po stejných, pouze navzájem posunutých trajektoriích
• Otáčivý (rotace) - všechny body tělesa se otáčejí kolem jedné společné osy se stejnou úhlovou rychlostí
• Složený (posuvný + otáčivý) - Složený rovinný pohyb bodu je pohyb bodu v rovině složený ze dvou nebo více současných rovinných pohybů, např. Dotahování šroubu

Moment síly

• vektorová fyzikální veličina vyjadřující otáčivý účinek síly $\vec F$ na tuhé těleso vektorová fyzikální veličina
• označí se $M$
• jednotka $N.m$

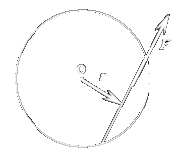
Momentová věta

$$M = \sum_{i = 1}^{n} M_i$$

a pokud se těleso neotáčí

$$M = 0 = \sum_{i = 1}^{n} M_i$$

Směr momentu sil

Směr momentu síly určíme podle pravidla pravé ruky:

Položíme-li pravou ruku na těleso tak, aby prsty ukazovaly směr otáčení tělesa, pak vztyčený palec ukazuje směr momentu síly.

Síly nejdříve přeneseme do společného bodu, kterým je průsečík jejich vektorových přímek, pak síly složíme doplněním na vektorový rovnoběžník a výslednou sílu $\vec F$ můžeme umístit do libovolného bodu její vektorové přímky síly.

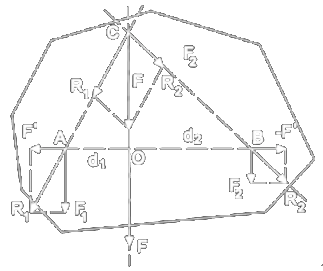
Zaměníme působiště obou sil a u jedné z nich změníme orientaci. Působiště výslednice je průsečíkem úsečky $AB$ se spojnicí koncových bodů přenesených sil. Výslednice sil má stejný směr jako dílčí síly a její velikost je dána součtem velikostí dílčích sil.

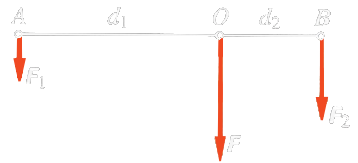
Těžiště tuhého tělesa

• Tuhé těleso je složeno z velkého počtu hmotných bod, jejichž vzájemná poloha se nemění. Na jednotlivé body působí tíhové síly $\vec F_{G1}$, $\vec F_{G2}$,…,$\vec F_{Gn}$, které jsou navzájem rovnoběžné. Jejich složením dostaneme výslednou tíhovou sílu $F_G$, která má působiště v bodě $T$, který nazýváme těžiště tělesa.
• Těžiště tuhého tělesa je působiště tíhové síly působící na těleso v homogenním tíhovém poli.

Určení polohy tělesa

• U stejnorodého geometrického pravidelného tělesa leží těžiště v jeho geometrickém středu (geometrickém těžišti)
• Těžiště leží v jeho v průsečíku těžnic při postupném zavěšení tělesa v nejméně dvou různých bodech

$$x_T = \frac{\sum m_i x_i}{m}$$

• jednotka [m]
• $m_i$ - hmotnost i-té části tělesa
• $x_i$ - poloha těžiště v i-té části tělesa
• $m$ - celková hmotnost

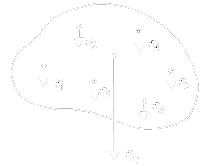
Podmínky rovnovážné polohy tuhého tělesa

Tuhé těleso je v rovnovážné poloze, jestliže se pohybový účinek všech sil působících na těleso navzájem ruší a těleso je v klidu.

• Podmínka rovnováhy sil
  • Těleso je v rovnovážné poloze, je-li výslednice všech sil působících na těleso nulová.
  $$F = \sum_{i = 1}^{n} F_n = 0$$
• Podmínka rovnováhy momentů sil
  • Těleso otáčivé kolem nehybné osy je v rovnovážné poloze, je-li vzhledem k této ose výsledný moment všech sil působících na těleso nulový. (tj. momentová věta)
  $$M = \sum_{i = 1}^{n} M_n = 0$$

Rovnovážné polohy tuhých těles

• Stálá (stabilní)
  • má těleso, které se po vychýlení z této polohy opět do ní vrací
  • např. hodíme-li míček do kopce a skutálí se zpět do původní polohy
• Vratká (labilní)
  • má těleso, které se po vychýlení z této polohy do ní nevrací, ale přechází do nové stálé polohy
  • např. hodíme-li míček z kopce a on se skutálí dolů, kde zůstane
• Volná (indiferentní)
  • má těleso, které zůstává po vychýlení v jakékoli nové poloze
  • např. pokud kopneme do míče na hřišti, míč pouze změní svoji polohu, nikoliv však potenciální energii

Kinetická energie tuhého tělesa

Kinetická energie tělesa je rovna součtu kinetických energií jednotlivých hmotných bodů

$$E_k = \sum_{i = 1}^{n} \frac{1}{2}m_iv_i$$ $$\downarrow$$ $$E_k = \sum_{i = 1}^{n} \frac{1}{2}m_i\omega^2r_i^2$$ $$\downarrow$$ $$E_k = \frac{1}{2}\omega^2 \left( \sum_{i = 1}^{n} m_ir_i^2 \right)$$

Moment setrvačnosti tuhého tělesa vzhledem k ose otáčení

• Moment setrvačnosti je skalární fyzikální veličina, která vyjadřuje rozložení látky v tělese vzhledem k ose otáčení
• Značí se $J$
• Jednotka [$kg.m^2$]

$$J = \sum_{i = 1}^{n} m_ir_i^2$$

Kinetická energie při otáčivém pohybu

$$E_k = \frac{1}{2}J\omega^2$$