MATFYZ

Foundations of Robotics (WIP)

[Edit]

If you find any error you can edit article using edit link ↑\uparrow.

References

History

Robots are old and in movies. There is also robotic fish.

Prehistory

There is book Leonardos robots. Japan had mechanic dolls.

Robotic structures

Three laws of robotics

1. Law
A robot may not injure a human being or, through inaction, allow a human being to come to harm

2. Law
A robot must obey orders given to it by human beings, except where such orders would conflict with the first law.

3. Law
A root must protect its own existence as long as such protection does not conflict with the first or second laws.

by Isaac Asimov, 1942, Runaround

Kinematics

Degrees of freedom (DOF)

Manipulators

Lower pair joints

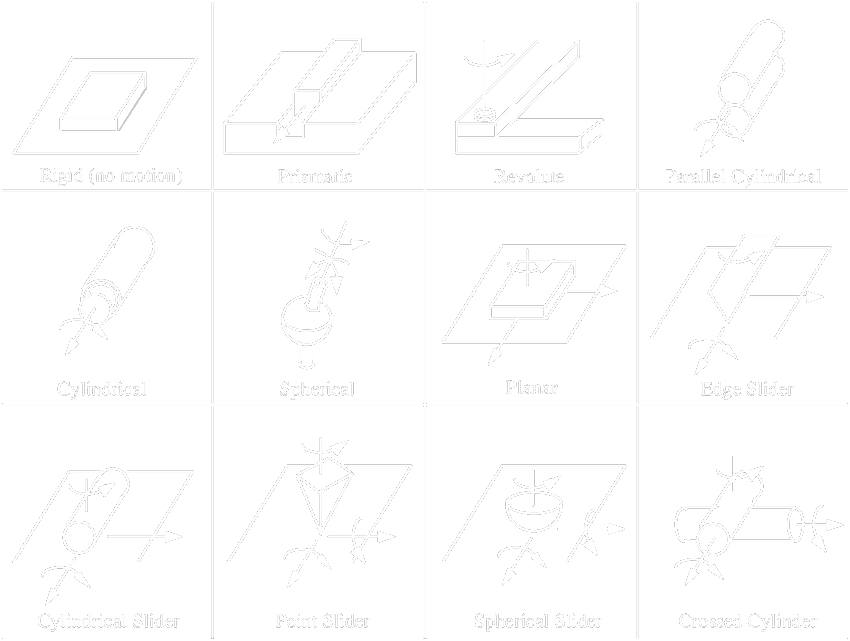
kinematics join types

Rotation

P′=R.PP' = R . P

Rotation xx axis, angle ϕ\phi

Rx,ϕ=[1000cos⁡ϕ−sin⁡ϕ0sin⁡ϕsin⁡ϕ]R_{x, \phi} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\phi & -\sin\phi \\ 0 & \sin\phi & \sin\phi \end{bmatrix}

Rotation yy axis, angle ψ\psi

Ry,ψ=[cos⁡ψ0sin⁡ψ010−sin⁡ψ0sin⁡ψ]R_{y, \psi} = \begin{bmatrix} \cos\psi & 0 & \sin\psi \\ 0 & 1 & 0 \\ -\sin\psi & 0 & \sin\psi \end{bmatrix}

Rotation zz axis, angle ξ\xi

Rz,ξ=[cos⁡ξ−sin⁡ξ0sin⁡ξsin⁡ξ0001]R_{z, \xi} = \begin{bmatrix} \cos\xi & -\sin\xi & 0 \\ \sin\xi & \sin\xi & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}

Rotation along xx,yy,zz by angles ϕ\phi, ψ\psi, ξ\xi

Rϕ,ψ,ξ=[cos⁡(ψ)cos⁡(ξ)−cos⁡(ψ)sin⁡(ξ)sin⁡(ψ)sin⁡(ϕ)sin⁡(ψ)cos⁡(ξ)−sin⁡(ϕ)sin⁡(ψ)sin⁡(ξ)+cos⁡(ϕ)sin⁡(ξ)+cos⁡(ϕ)cos⁡(ξ)−sin⁡(ϕ)cos⁡(ψ)−cos⁡(ϕ)sin⁡(ψ)cos⁡(ξ)cos⁡(ϕ)sin⁡(ψ)sin⁡(ξ)cos⁡(ϕ)cos⁡(ψ)+sin⁡(ϕ)sin⁡(ξ)+sin⁡(ϕ)cos⁡(ξ)]R_{\phi, \psi, \xi}=\left[\begin{array}{ccc} \cos (\psi) \cos (\xi) & -\cos (\psi) \sin (\xi) & \sin (\psi) \\ {} & {} & {} \\ \sin (\phi) \sin (\psi) \cos (\xi) & -\sin (\phi) \sin (\psi) \sin (\xi) & \\ +\cos (\phi) \sin (\xi) & +\cos (\phi) \cos (\xi) & -\sin (\phi) \cos (\psi) \\ & & \\ -\cos (\phi) \sin (\psi) \cos (\xi) & \cos (\phi) \sin (\psi) \sin (\xi) & \cos (\phi) \cos (\psi) \\ +\sin (\phi) \sin (\xi) & +\sin (\phi) \cos (\xi) & \end{array}\right]

Homogenní souřadnice

Bod p=(x,y,z,w)T,x,y,z∈R,w=1p = (x,y,z,w)^{T}, x,y,z \in \R, w = 1

2D Rotation

(x′,y′,w′)T=[cos⁡(α)−sin⁡(α)0sin⁡(α)cos⁡(α)0001][xyw]\left(x^{\prime}, y^{\prime}, w^{\prime}\right)^{T}= \left[\begin{array}{ccc} \cos (\alpha) & -\sin (\alpha) & 0 \\ \sin (\alpha) & \cos (\alpha) & 0 \\ 0 & 0 & 1 \end{array}\right] \begin{bmatrix}x \\ y \\ w\end{bmatrix}

2D Translation

(x′,y′,w′)T=[10dx01dy001][xyw]\left(x^{\prime}, y^{\prime}, w^{\prime}\right)^{T}= \left[\begin{array}{ccc} 1 & 0 & d_{x} \\ 0 & 1 & d_{y} \\ 0 & 0 & 1 \end{array}\right] \begin{bmatrix}x \\ y \\ w\end{bmatrix}

Rotation + translation

P′=R⋅P+T→P′=T.PP^{\prime}=R \cdot P + T \rightarrow P^{\prime} = \Tau . P

[P′1]=[RT0⋯01]⋅P\begin{bmatrix} P' \\ 1 \end{bmatrix} = \begin{bmatrix} R & T \\ 0\cdots0 & 1 \end{bmatrix} \cdot P [x′y′z′1]=[[□□□□□□□□□]txtytz0001]⋅[xyz1]\begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} \begin{bmatrix} \square & \square & \square \\ \square & \square & \square \\ \square & \square & \square \\ \end{bmatrix} &\kern-1em \begin{array}{c} t_{x} \\ t_{y} \\ t_{z} \end{array} \\ 0 \kern1.3em 0 \kern1.3em 0 &\kern-1em 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}

Forward kinematics (3D)

System composition

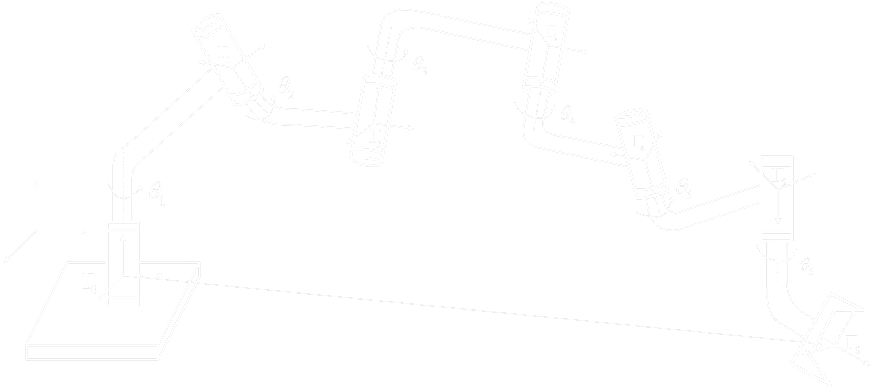
DH example

Denavit-Hartengerg

Fictive movements which connect two systems:

rotate, move, move, rotate.

That can be generalized to any sequence.

tsc

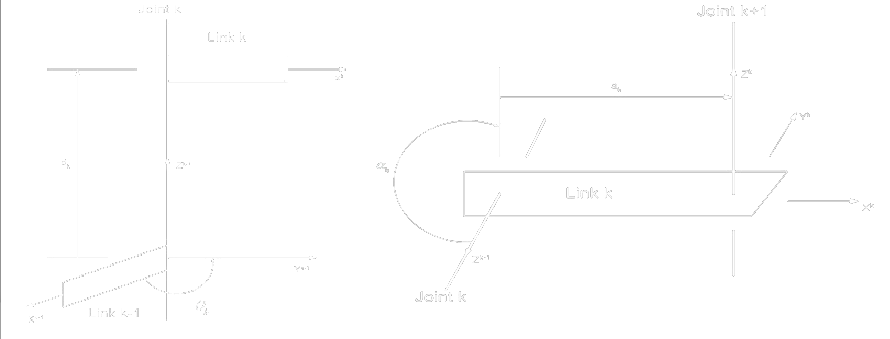
Denavit-Hartenberg overview

Definice

Relation between LCSi−1L C S_{i-1} and LCSiL C S_{i} is a composed transformation:

1. Rotate xi−1x_{i-1} axis along zi−1z_{i-1} by angle ϑi\vartheta_{i} Azi−1,ϑiA_{z_{i-1},\vartheta_{i}}
2. Translate xi−1x_{i-1} axis towards zi−1z_{i-1} by distance did_{i} Azi−1,diA_{z_{i-1}, d_{i}}
3. Translate LCSi−1L C S_{i-1} along xix_{i} axis by distance aia_{i} Ax,aiA_{x, a_{i}}
4. Rotate zi−1z_{i-1} axis along xix_{i} by angle αi\alpha_{i} Ax,αiA_{x, \alpha_{i}}

DH parameters: ϑi,di,ai,αi\vartheta_{i}, d_{i}, a_{i}, \alpha_{i}

lcs example

DH transformation

  1. Rotate xi−1x_{i-1} axis along zi−1z_{i-1} by angle ϑi\vartheta_{i}

    Azi−1,ϑi=[cos⁡(ϑi)−sin⁡(ϑi)00sin⁡(ϑi)cos⁡(ϑi)0000100001]A_{z_{i-1}, \vartheta_{i}}=\left[\begin{array}{cccc} \cos \left(\vartheta_{i}\right) & -\sin \left(\vartheta_{i}\right) & 0 & 0 \\ \sin \left(\vartheta_{i}\right) & \cos \left(\vartheta_{i}\right) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]

  2. Translate xi−1x_{i-1} axis towards zi−1z_{i-1} by distance did_{i}

    Azi−1,di=[10000100001di0001]A_{z_{i-1}, d_{i}}=\left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & d_{i} \\ 0 & 0 & 0 & 1 \end{array}\right]

  3. Translate LCSi−1L C S_{i-1} along xix_{i} axis by distance aia_{i}

    Axi,ai=[100ai010000100001]A_{x_{i}, a_{i}}=\left[\begin{array}{cccc} 1 & 0 & 0 & a_{i} \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]

  4. Rotate zi−1z_{i-1} axis along xix_{i} by angle αi\alpha_{i}

    Azi−1,di=[10000cos⁡(αi)−sin⁡(αi)00sin⁡(αi)cos⁡(αi)00001]A_{z_{i-1}, d_{i}}=\left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos \left(\alpha_{i}\right) & -\sin \left(\alpha_{i}\right) & 0 \\ 0 & \sin \left(\alpha_{i}\right) & \cos \left(\alpha_{i}\right) & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]

Finálně vše zkombinujeme

Ai−1i=Azi−1,ϑi⋅Azi−1,di⋅Ax,ai⋅Ax,αiA_{i-1}^{i}=A_{z_{i-1}, \vartheta_{i}} \cdot A_{z_{i-1}, d_{i}} \cdot A_{x, a_{i}} \cdot A_{x, \alpha_{i}} Ai−1i=[cos⁡(ϑi)−sin⁡(ϑi)cos⁡(αi)sin⁡(ϑi)sin⁡(αi)aicos⁡(ϑi)sin⁡(ϑi)cos⁡(ϑi)cos⁡(αi)−cos⁡(ϑi)sin⁡(αi)aisin⁡(ϑi)0sin⁡(αi)cos⁡(αi)di0001]A_{i-1}^{i}= \left[\begin{array}{cccc} \cos \left(\vartheta_{i}\right) & -\sin \left(\vartheta_{i}\right) \cos \left(\alpha_{i}\right) & \sin \left(\vartheta_{i}\right) \sin \left(\alpha_{i}\right) & a_{i} \cos \left(\vartheta_{i}\right) \\ \sin \left(\vartheta_{i}\right) & \cos \left(\vartheta_{i}\right) \cos \left(\alpha_{i}\right) & -\cos \left(\vartheta_{i}\right) \sin \left(\alpha_{i}\right) & a_{i} \sin \left(\vartheta_{i}\right) \\ 0 & \sin \left(\alpha_{i}\right) & \cos \left(\alpha_{i}\right) & d_{i} \\ 0 & 0 & 0 & 1 \end{array}\right]

Ai−1iA^i_{i-1} usage

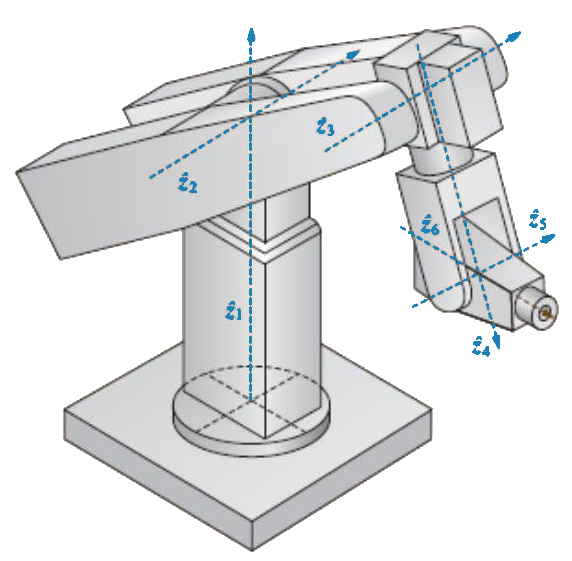
DH system construction

Motion model

Holonomic / non-holonomic drive

Definice

A vehicle is holonomic if the number of local degrees of freedom of movement equals the number of global degrees of freedom.

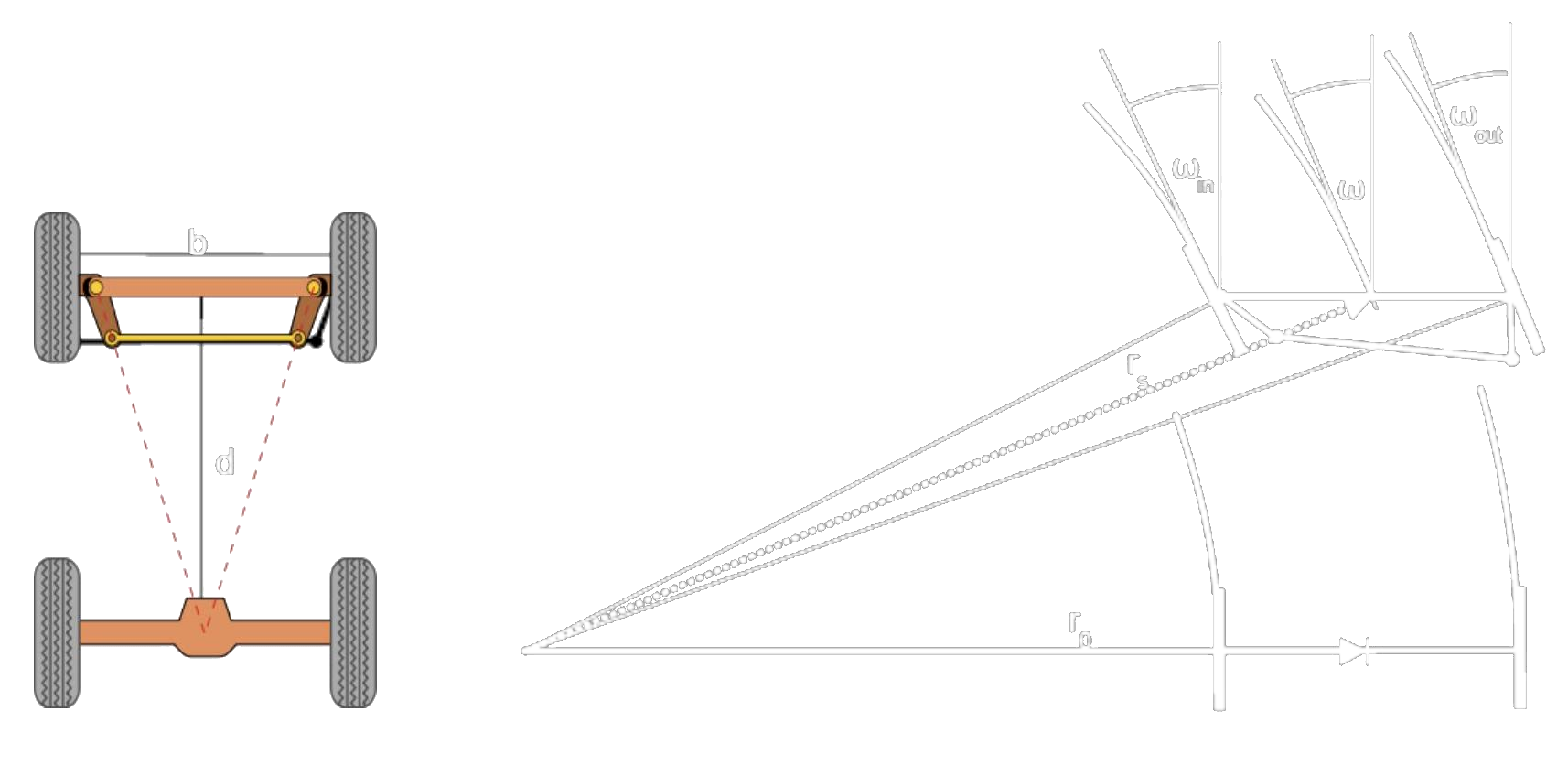
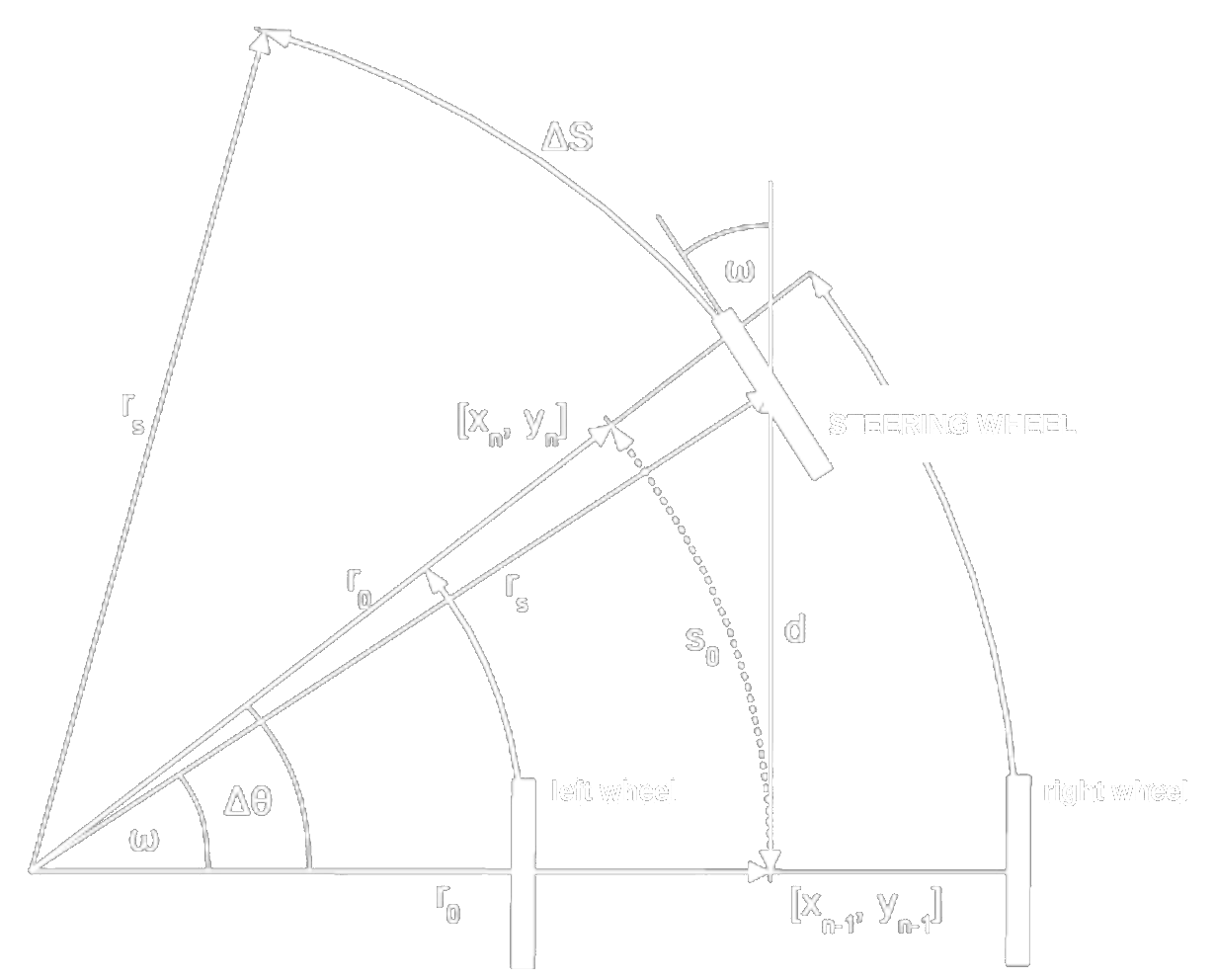
Ackermann steering

Ackeermann steering example Ackermann steering diagram
Basic principle Simplified model

Differential steering

rn=b2ΔR+ΔLΔR−ΔLr_{n}=\frac{b}{2} \frac{\Delta R+\Delta L}{\Delta R-\Delta L} Δθ=Snrn=ΔR+ΔL2b2ΔR+ΔLΔR−ΔL=ΔR−ΔLb\Delta \theta =\frac{S_{n}}{r_{n}}=\frac{\frac{\Delta R+\Delta L}{2}}{\frac{b}{2} \frac{\Delta R+\Delta L}{\Delta R-\Delta L}}=\frac{\Delta R-\Delta L}{b} xn=xn−1+Sn[cos⁡(Δθ+θn−1)]yn=yn−1+Sn[sin⁡(Δθ+θn−1)]\begin{aligned} x_{n} & =x_{n-1}+S_{n}\left[\cos \left(\Delta \theta+\theta_{n-1}\right)\right] \\ y_{n} & =y_{n-1}+S_{n}\left[\sin \left(\Delta \theta+\theta_{n-1}\right)\right] \end{aligned} x(t)=x0+b(vr+vl)2(vr−vl)[sin⁡((vr−vl)t/b+θ)−sin⁡(θ)]y(t)=y0+b(vr+vl)2(vr−vl)[cos⁡((vr−vl)t/b+θ)−cos⁡(θ)]\begin{aligned} x(t)&=x_{0}+\frac{b\left(v_{r}+v_{l}\right)}{2\left(v_{r}-v_{l}\right)}\left[\sin \left(\left(v_{r}-v_{l}\right) t / b+\theta\right)-\sin (\theta)\right] \\ y(t)&=y_{0}+\frac{b\left(v_{r}+v_{l}\right)}{2\left(v_{r}-v_{l}\right)}\left[\cos \left(\left(v_{r}-v_{l}\right) t / b+\theta\right)-\cos (\theta)\right] \end{aligned}

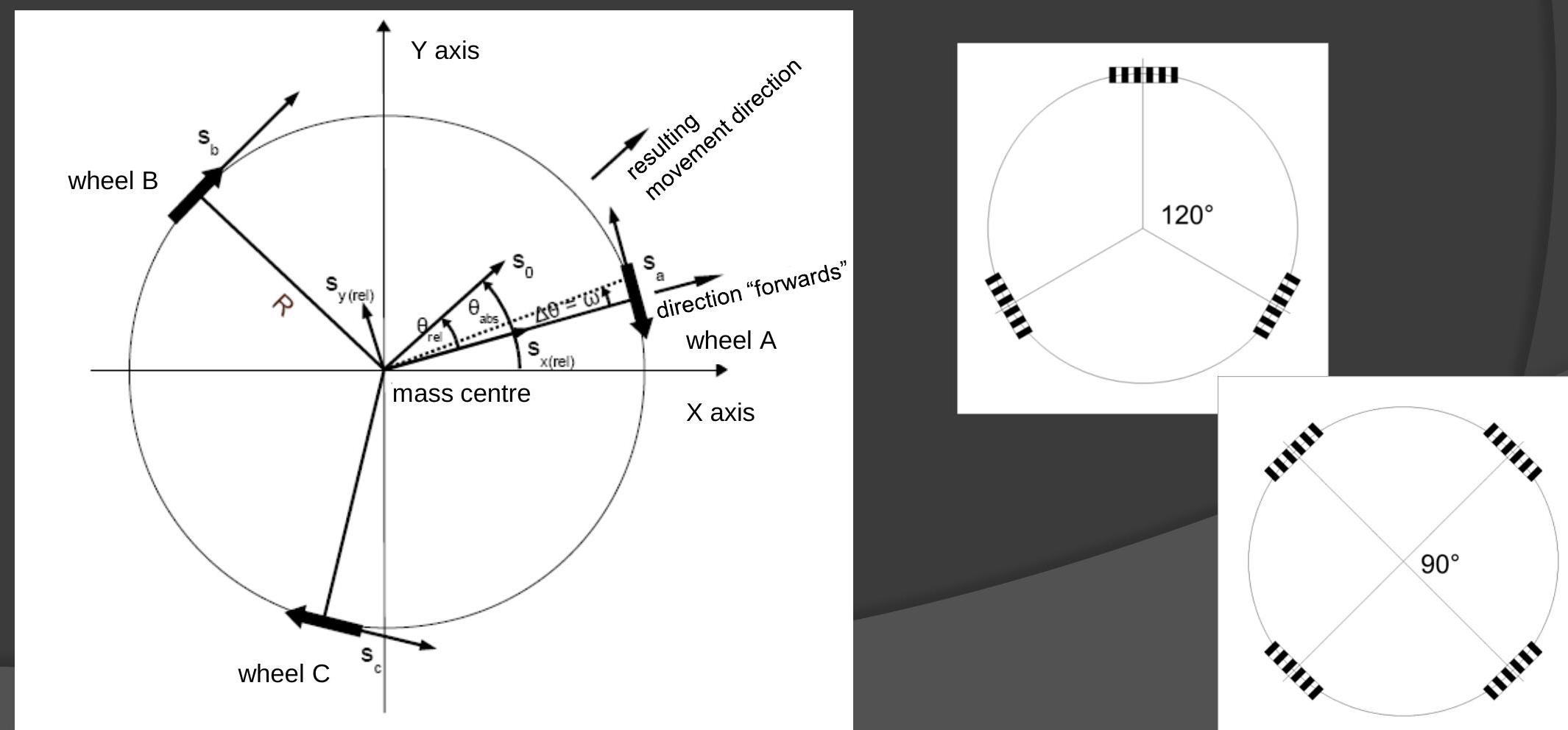
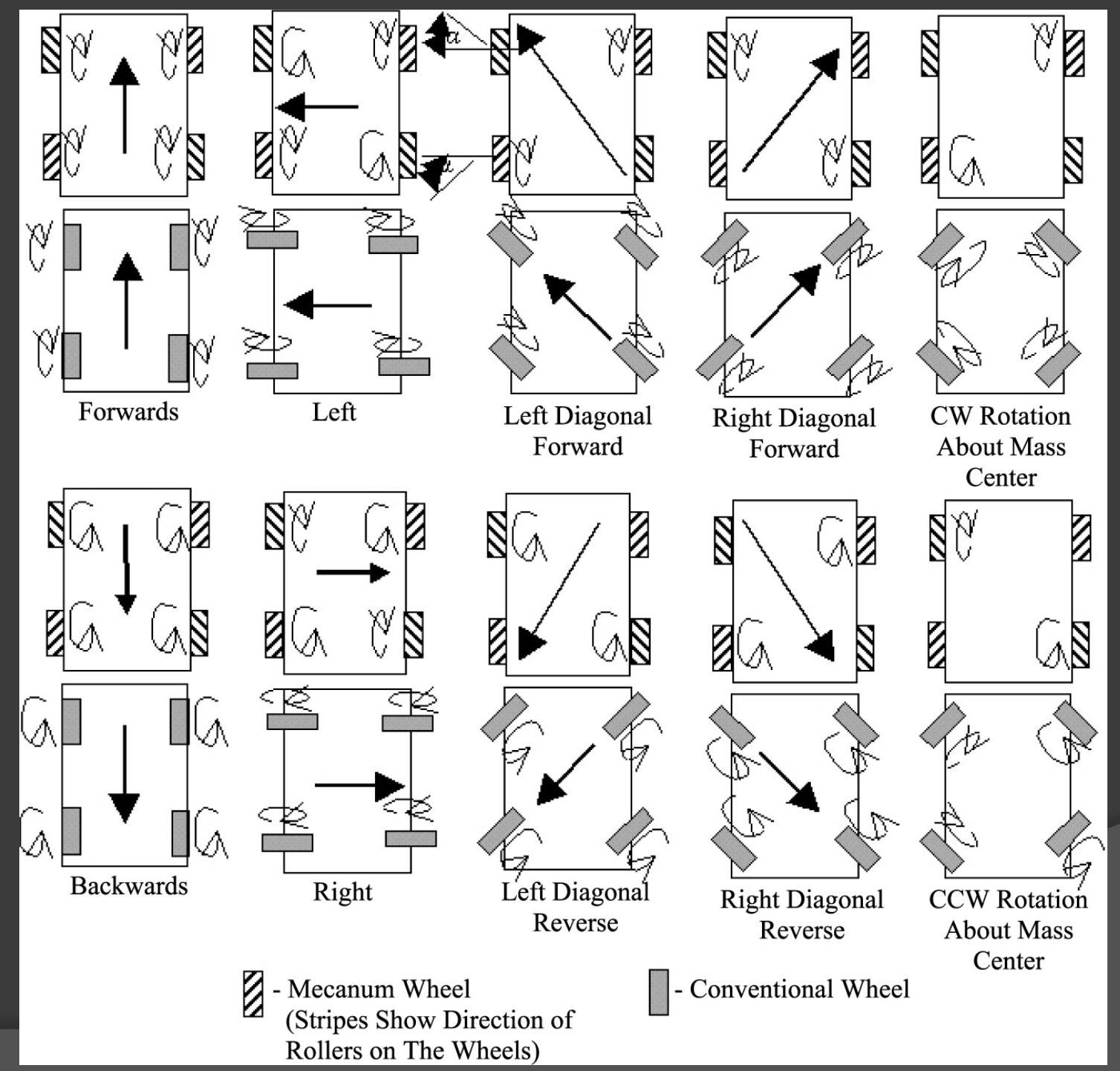
Omnidirectional steering

Omniwheel examples 1
Omniwheel examples 2

syncro drive

1. Holonomic

Holonomic movement

2. Killough / Ilon wheels

Killough movement scheme Killough movement example

3. Omniwheel drive

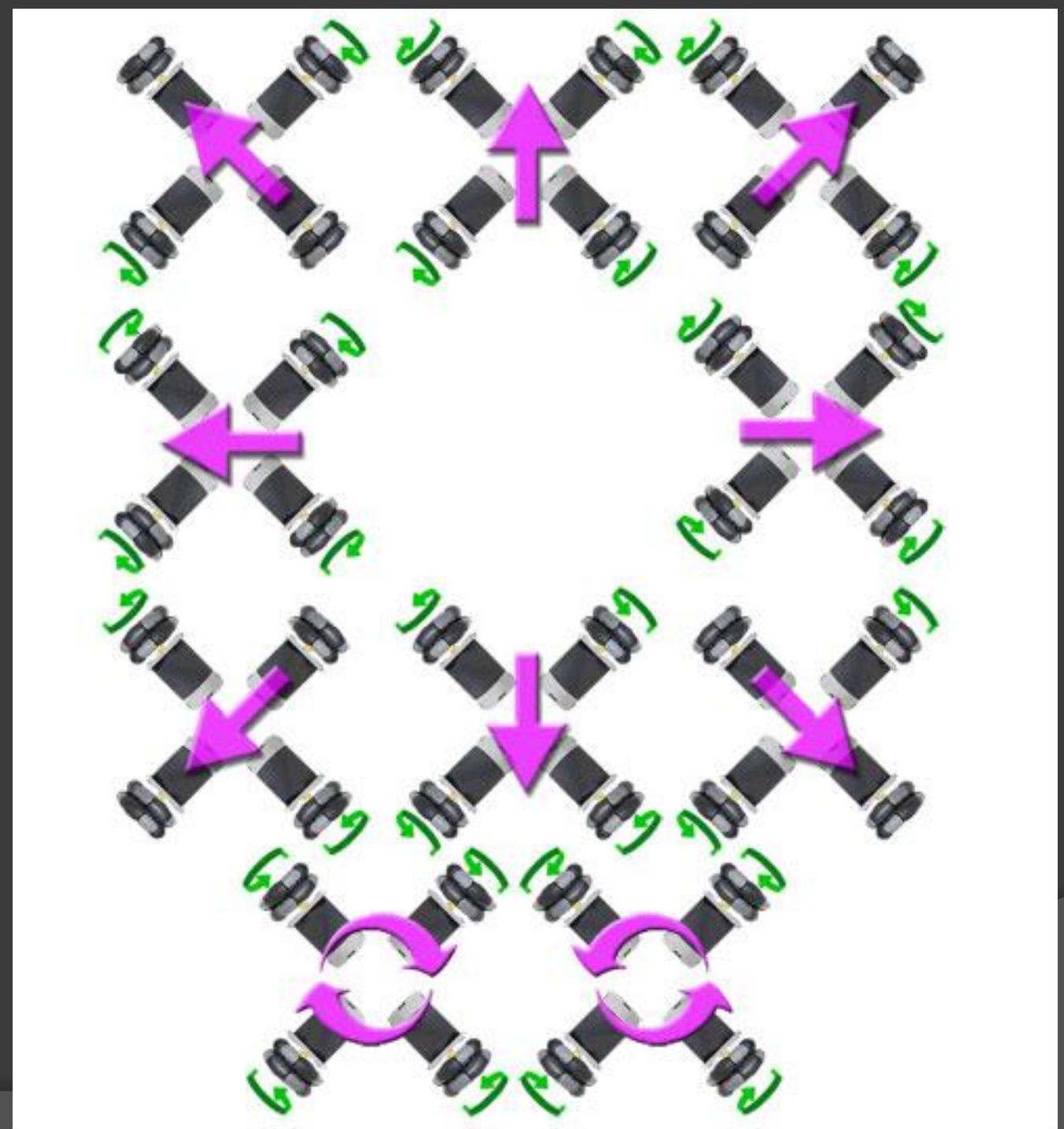
Omniwheel direction visualised

Mecanum \& swerve drive

Mecanum drive

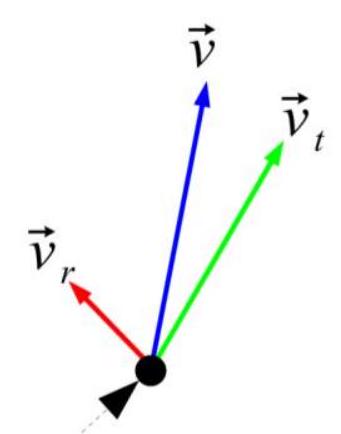
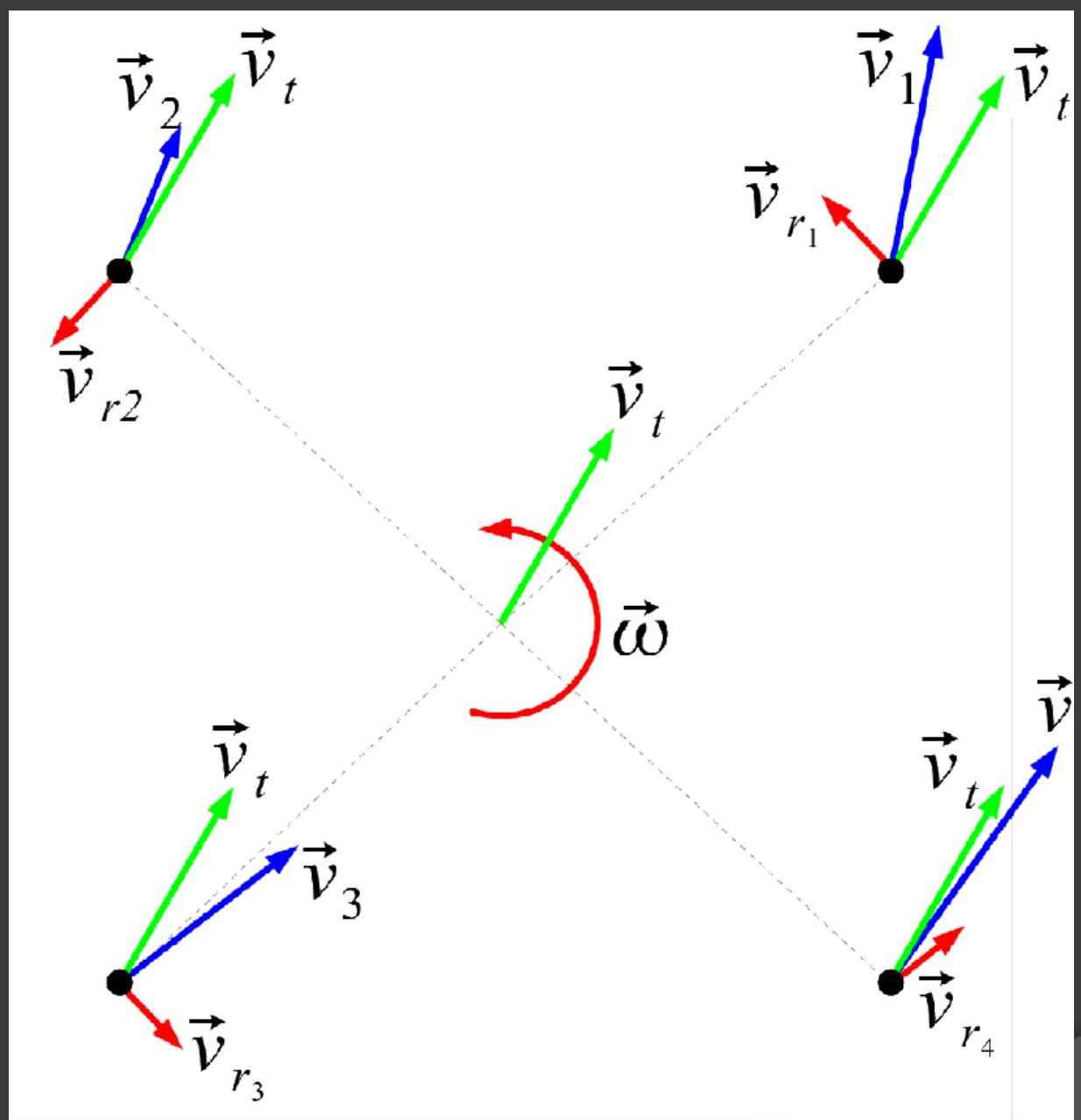
Robot movement

robot movement scheme 1 robot movement scheme 2

Swerve drive

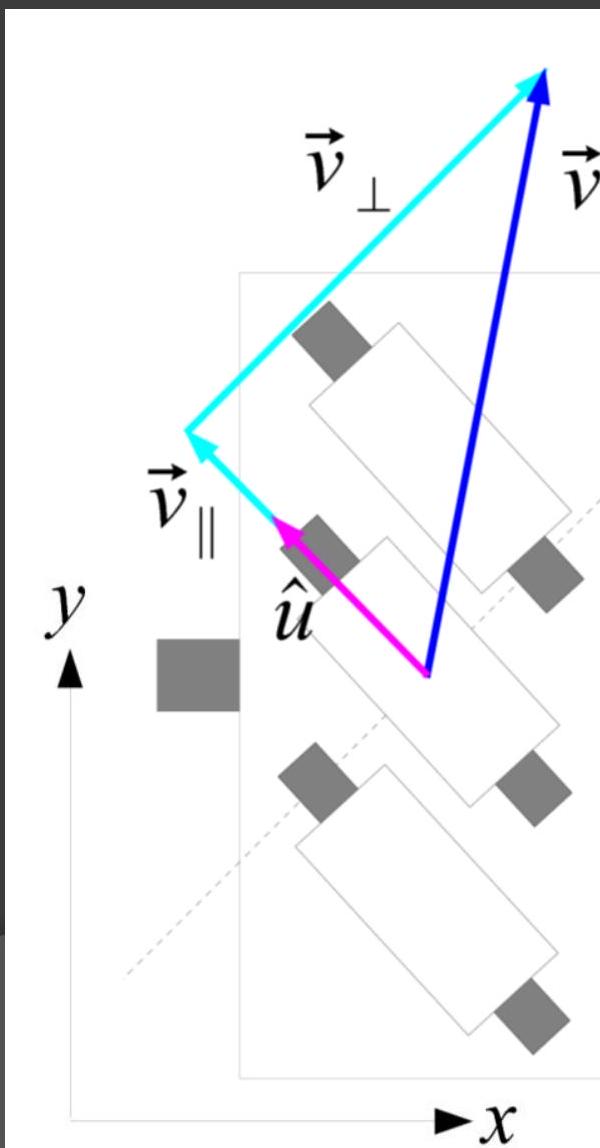
  • Resolve vt→\overrightarrow{v_{t}} (xx, yy components = axes velocities ) into wheel speed vwv_{w} and steering angle θ\theta
vω=vx2+vy2θ=arctan⁡(vyvx)\begin{aligned} v_{\omega} &=\sqrt{v_{x}^{2}+v_{y}^{2}} \\ \theta &=\arctan \left(\frac{v_{y}}{v_{x}}\right) \end{aligned}
  • Resolve velocity into parallel and perpendicular components; magnitude vv of parallel component is wheel speed vwv_{w}
  • u^\hat{u} is a unit vector in the direction of the wheel (whichever direction is assumed to be “forwards”)
vw=v∥=v⃗⋅u^=(vxı^+vyȷ^)⋅(−12ı^+12ȷ^)=−12vx+12vy\begin{aligned} v_{w} &= v_{\|}=\vec{v} \cdot \hat{u} \\ &=\left(v_{x} \hat{\imath}+v_{y} \hat{\jmath}\right) \cdot\left(-\frac{1}{\sqrt{2}} \hat{\imath}+\frac{1}{\sqrt{2}} \hat{\jmath}\right) \\ &=-\frac{1}{\sqrt{2}} v_{x}+\frac{1}{\sqrt{2}} v_{y} \end{aligned}

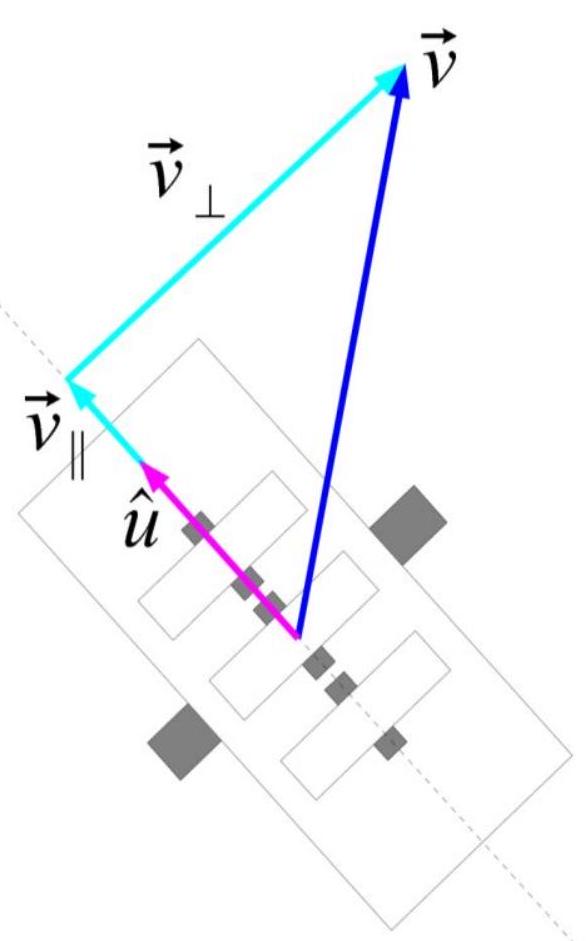
swerve drive

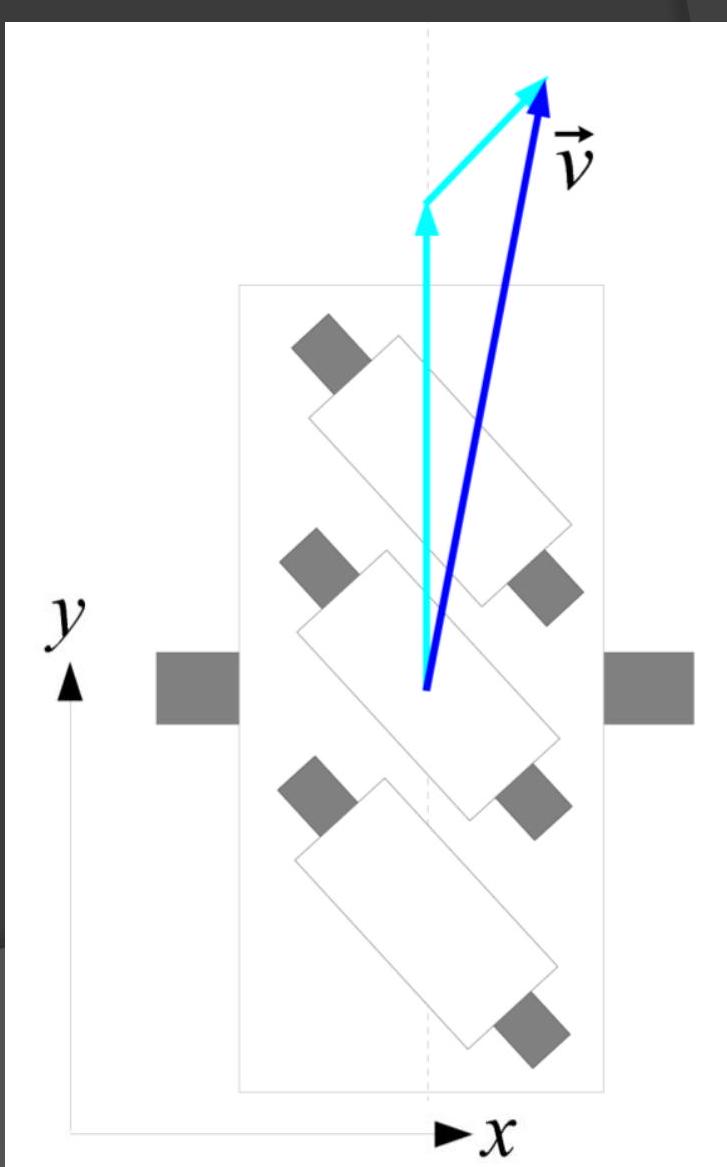
Mecanum drive

  • Similar to omniwheel drive
  • Conceptually: Resolve velocity into components parallel to wheel and parallel to roller
  • Not easy to calculate directly (directions are not perpendicular), so do it in two steps:
  • Resolve to roller
  • Resolve to wheel

Mecanum drive wheel 1

  • Resolve velocity into components parallel and perpendicular to roller axis
  • u^\hat{u} is not the same for each wheel; pick direction parallel to roller axis, in forwards direction
  • Perpendicular component can be discarded
v∥=v⃗⋅u^v_{\|}=\vec{v} \cdot \hat{u} =(vxı^+vyȷ^)⋅(−12ı^+12ȷ^)=\left(v_{x} \hat{\imath}+v_{y} \hat{\jmath}\right) \cdot\left(-\frac{1}{\sqrt{2}} \hat{\imath}+\frac{1}{\sqrt{2}} \hat{\jmath}\right)

mecanum drive wheel 2

  • Use component parallel to roller axis and resolve it into components parallel to wheel and parallel to roller
  • vwv_{w} is the component parallel to the wheel
  • When the angle is known, we can calculate vwv_{w} directly.
    • E.g. for 45∘45^{\circ} inclination:
vw=v∥cos⁡45∘=2(−12vx+12vy)=−vx+vy\begin{aligned} v_{w} & =\frac{v_{\|}}{\cos 45^{\circ}} \\ & =\sqrt{2}\left(-\frac{1}{\sqrt{2}} v_{x}+\frac{1}{\sqrt{2}} v_{y}\right) \\ & =-v_{x}+v_{y} \end{aligned}

mecanum drive wheel 3

Localization

Coordinate transformation

Absolute localization

Relative localization

Dead reckoning

Odometry

Robot centric sensors

Most sensors move with the robot, so we have to do further data processing (e.g. recalculate coordinates relative to the global system,…\ldots).

Types of localization

A possible solutions

  1. More accurate measurement - better sensors and actuators, data filtering, the most accurate model of the robot and the environment
  2. Do not rely on the fact that localization is accurate - probabilistic methods, fuzzy logic, interval algebra
    • We can consider the data as random variables (inputs, pose)
    • The position estimate is then a distribution
    • Localization is then the search for a distribution that best matches the real position of the robot
    • In 1D Belief Bel(x)Bel(x) where ∫−∞∞Bel(x)dx=1\int_{-\infty}^{\infty}Bel(x)dx=1 Ideally, Bel(x)=1Bel(x) = 1 for exact but we can’t reach the position
    • We want to model Bel(x)=P(x∣l1,…,lk)Bel(x) = P(x\mid l_{1},\dots,l_{k})
    • Random modeling can be used with particle filters, Bayesian methods,…
    • We estimate the posterior by measuring the prior
Representation
Probability Grid
Topological graphs
Monte Carlo localization
Continuous representation (Kalman filter)
Other methods

Solution 3 no localization

SLAM

Satellite localization

If we know the distance of the aiming point from the satellite, it will determine the sphere. Two specifies a circle and three a point. In practice, at least four satellites are typically used.

Simple idea: measuring the signal time-of-flight →\rightarrow distance

History

GPS satellites

Competitive global systems

Compass(China), Galileo(EU), GLONASS(Russia)

Regional systems

Beidou(China), DORIS(France), IRNSS(India)

Local systems

Galileo

European project, more accurate (about 1 m)

Ublox

Indoor GPS

Environment representation

Maps

we divide according to several aspects

Types of maps

Planning

Prerequisites

Description of the problem

Scheduling algorithms

Bug algorithm

Prerequisites bug alg

Bug 0

Bug 1

Bug 2

Go to the goal, if you come across an obstacle, go around it until you can’t go straight to the goal again

Lemma

Bug 2 finally encounters many obstacles and passes them all through the start-finish junction

Bug 2 passes each point on the obstacle at most ni2\frac{n_i}{2} times, where nin_i is the number of crossings of the obstacle ii with the start-finish line.

∣target−start∣+∑i=1Nni⋅pi2\lvert \text{target} - \text{start} \rvert + \sum_{i=1}^{N}\frac{n_i\cdot p_i}{2}

Comparison of Bug 1 and Bug 2 (TODO)

There are cases for which 1 is better than two and vice versa

Estimates for length can be improved if the robot can see some of its surroundings (area inside the circle around itself)

Tangent bug

selects by angle of direction to direction to target (TODO) It is correct

Dijkstra

alternative path search A* is a Dijkstra + heuristic, if the heuristic satisfies something it can be proven that it does not process vertices twice. E.g. price + distance from destination D* also handles replanning when an obstacle appears, starting from the destination

Rapidly exploring random trees

Randomized algorithm It quickly finds some solution and iteratively adjusts

Potential field

The robot is in sweat. fields, obstacles are peaks - repel the goal is the minimum

Multirobot systems

Why use multirobot systems

Types of systems

Satellite localization

If we know the distance of the aiming point from the satellite, it will determine the sphere. Two specifies a circle and three a point. In practice, at least four satellites are typically used.

Simple idea: measuring the signal time-of-flight →\rightarrow distance

History

GPS satellites

Competitive global systems

Compass(China), Galileo(EU), GLONASS(Russia)

Regional systems

Beidou(China), DORIS(France), IRNSS(India)

Local systems

Galileo

European project, more accurate (about 1 m)

Ublox

Indoor GPS