Malý tahák k diferenciálním a integrálním počtům
Úvod
Diferenciálními a integrálními počty se zabývá obor Matematická analýza .
Funkce
Definice funkce : Funkce je relace R R R X X X Y Y Y x ∈ X x \in X x ∈ X y ∈ Y y \in Y y ∈ Y ( x , y ) ∈ R (x,y) \in R ( x , y ) ∈ R
značení funkce z množiny X X X Y Y Y
f : X → Y f: X \to Y f : X → Y Definiční obor
Definiční obor funkce je množia všech přípustných hodnot, které můžeme ve funkci f ( x ) f(x) f ( x )
D f = { x ∈ X ∣ ( ∃ Y ∈ X ) ( f ( x ) = y ) } D_f = \{ x \in X |( \exists Y \in X)(f(x) = y)\} D f = { x ∈ X ∣ ( ∃ Y ∈ X ) ( f ( x ) = y )} Obor hodnot
Obor hodnot je množina všech hodnot, kterých může f ( x ) f(x) f ( x )
H f = { y ∈ Y ∣ ( ∃ x ∈ X ) ( f ( x ) = y ) } H_f = \{ y \in Y |( \exists x \in X)(f(x) = y)\} H f = { y ∈ Y ∣ ( ∃ x ∈ X ) ( f ( x ) = y )} Druhy zobrazení
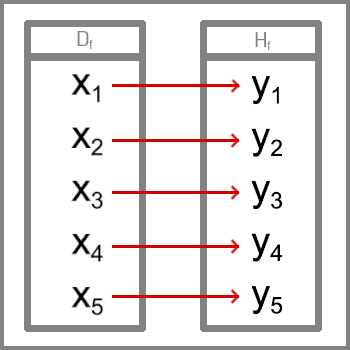
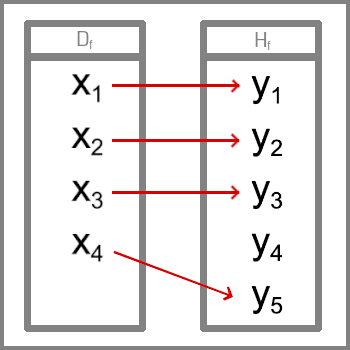
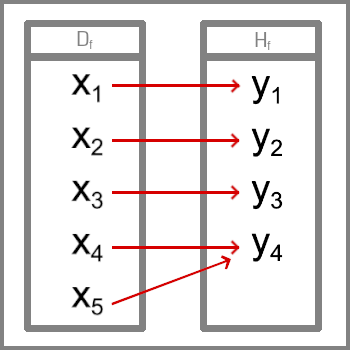
Bijekce - ke každému x x x y y y Injekce - Ke každému y y y x x x Surjekce - Ke každému y y y x x x
Interval monotónosti
Funkce f f f ( a ; b ) (a;b) ( a ; b )
rostoucí ⟺ ∀ x 1 , x 2 ∈ ( a ; b ) , x 1 < x 2 : f ( x 1 ) < f ( x 2 ) \iff \forall x_1, x_2 \in (a;b) , x_1 < x_2 : f(x_1) < f(x_2) ⟺ ∀ x 1 , x 2 ∈ ( a ; b ) , x 1 < x 2 : f ( x 1 ) < f ( x 2 )
neklesající ⟺ ∀ x 1 , x 2 ∈ ( a ; b ) , x 1 < x 2 : f ( x 1 ) ≤ f ( x 2 ) \iff \forall x_1, x_2 \in (a;b) , x_1 < x_2 : f(x_1) \leq f(x_2) ⟺ ∀ x 1 , x 2 ∈ ( a ; b ) , x 1 < x 2 : f ( x 1 ) ≤ f ( x 2 )
klesající ⟺ ∀ x 1 , x 2 ∈ ( a ; b ) , x 1 < x 2 : f ( x 1 ) > f ( x 2 ) \iff \forall x_1, x_2 \in (a;b) , x_1 < x_2 : f(x_1) > f(x_2) ⟺ ∀ x 1 , x 2 ∈ ( a ; b ) , x 1 < x 2 : f ( x 1 ) > f ( x 2 )
nerostoucí ⟺ ∀ x 1 , x 2 ∈ ( a ; b ) , x 1 < x 2 : f ( x 1 ) ≥ f ( x 2 ) \iff \forall x_1, x_2 \in (a;b) , x_1 < x_2 : f(x_1) \geq f(x_2) ⟺ ∀ x 1 , x 2 ∈ ( a ; b ) , x 1 < x 2 : f ( x 1 ) ≥ f ( x 2 )
Sudost/Lichost
Funkce f f f ⟺ f ( x ) = − f ( x ) \iff f(x) = -f(x) ⟺ f ( x ) = − f ( x )
Funkce f f f ⟺ f ( x ) = f ( − x ) \iff f(x) = f(-x) ⟺ f ( x ) = f ( − x )
Funkce není sudá ani lichá pokud neplatí ani jedna z předchozích vlastností
Průsečíky s osami
Průsečík P P P P ∈ P \in P ∈ ∩ H f \cap H_f ∩ H f
Průsečík s osou Y
Existuje nejvýše jeden průsečík s osou Y. (Vychází z definice funkce)
pro průsečík P Y P_Y P Y P Y = [ 0 ; f ( 0 ) ] P_Y = [0; f(0)] P Y = [ 0 ; f ( 0 )]
Průsečík s osou X
pro průsečík P X P_X P X P X = [ x ; 0 ] ; f ( x ) = 0 P_X = [x; 0] ; f(x) = 0 P X = [ x ; 0 ] ; f ( x ) = 0
Příklady základních funkcí
Funkce
Příklad grafu
Konstanttní funkce: f : y = c f: y = c f : y = c D f = R D_f = \R D f = R H f = { c } H_f = \{c\} H f = { c }
Lineární funkce: f : y = a x + b f: y = ax + b f : y = a x + b D f = R D_f = \R D f = R H f = R H_f = \R H f = R
Kvadratická funkce: f : y = a x 2 + b x + c f: y = ax^2 + bx + c f : y = a x 2 + b x + c D f = R D_f = \R D f = R
Kubická funkce: f : y = a x 3 + b x 2 + c x + d f: y = ax^3 + bx^2 +cx + d f : y = a x 3 + b x 2 + c x + d D f = R D_f = \R D f = R H f = R H_f = \R H f = R
Exponenciální funkce: f : y = c x f: y = c^x f : y = c x D f = R D_f = \R D f = R H f = R + H_f = \R^+ H f = R +
Logaritmická funkce: f : y = log a x f: y = \log_a x f : y = log a x D f = R + D_f = \R^+ D f = R + H f = R H_f = \R H f = R
Absolutní hodnota: f : y = ∣ x ∣ f: y = |x| f : y = ∣ x ∣ D f = R D_f = \R D f = R H f = R + ∪ { 0 } H_f = \R^+ \cup \{0\} H f = R + ∪ { 0 }
Limita
lim x → a f ( x ) = L ⟺ ∀ ϵ ∈ R + ∃ Δ ∈ R + ∀ x ∈ O Δ ( a ) ∧ x ≠ a ; f ( x ) ∈ O ϵ ( L ) ; \lim_{x \to a} f(x) = L \iff \forall \epsilon \in \R^+ \exists \Delta \in \R^+ \forall x \in O_{\Delta}(a) \land x \neq a; f(x) \in O_{\epsilon}(L); lim x → a f ( x ) = L ⟺ ∀ ϵ ∈ R + ∃Δ ∈ R + ∀ x ∈ O Δ ( a ) ∧ x = a ; f ( x ) ∈ O ϵ ( L ) ; x ∈ ( a − Δ ; a + Δ ) ; f ( x ) ∈ ( L − ϵ ; L + ϵ ) x \in (a - \Delta; a + \Delta); f(x) \in (L - \epsilon; L + \epsilon) x ∈ ( a − Δ ; a + Δ ) ; f ( x ) ∈ ( L − ϵ ; L + ϵ )
lim x → ∞ f ( x ) = L ⟺ ∀ ϵ ∈ R + ∃ x 0 ∈ D f ∀ x > x 0 ; ∣ f ( x ) − L ∣ < ϵ \lim_{x \to \infty} f(x) = L \iff \forall \epsilon \in \R^+ \exists x_0 \in D_f \forall x > x_0 ; | f(x) -L | < \epsilon x → ∞ lim f ( x ) = L ⟺ ∀ ϵ ∈ R + ∃ x 0 ∈ D f ∀ x > x 0 ; ∣ f ( x ) − L ∣ < ϵ lim x → − ∞ f ( x ) = L ⟺ ∀ ϵ ∈ R + ∃ x 0 ∈ D f ∀ x < x 0 ; ∣ f ( x ) − L ∣ < ϵ \lim_{x \to -\infty} f(x) = L \iff \forall \epsilon \in \R^+ \exists x_0 \in D_f \forall x < x_0 ; | f(x) - L | < \epsilon x → − ∞ lim f ( x ) = L ⟺ ∀ ϵ ∈ R + ∃ x 0 ∈ D f ∀ x < x 0 ; ∣ f ( x ) − L ∣ < ϵ
Limita vlastní
Limita je vlastní ⟺ lim x → a f ( x ) ∈ R \iff \lim_{x \to a} f(x) \in \R ⟺ lim x → a f ( x ) ∈ R
Limita nevlastní
Limita je nevlastní ⟺ lim x → a f ( x ) ∈ { − ∞ ; ∞ } \iff \lim_{x \to a} f(x) \in \{-\infty;\infty\} ⟺ lim x → a f ( x ) ∈ { − ∞ ; ∞ }
Limita ve vlastním bodě
Funkce f f f ⟺ x ∈ D f \iff x \in D_f ⟺ x ∈ D f
Limity v nekonečnu
lim x → ∞ x n = ∞ \lim_{x \to \infty} x^n = \infty x → ∞ lim x n = ∞ lim x → ∞ a x n = 0 \lim_{x \to \infty} \frac{a}{x^n} = 0 x → ∞ lim x n a = 0 lim x → ∞ x a = ∞ \lim_{x \to \infty} \sqrt[a]{x} = \infty x → ∞ lim a x = ∞ lim x → ∞ a x = ∞ ⟺ a > 1 \lim_{x \to \infty} a^x = \infty \iff a > 1 x → ∞ lim a x = ∞ ⟺ a > 1 Spojitost
Funkce f ( x ) f(x) f ( x ) a ⟺ lim x → a f ( x ) = f ( a ) a \iff \lim_{x \to a}f(x) = f(a) a ⟺ lim x → a f ( x ) = f ( a )
Funkce f ( x ) f(x) f ( x ) ⟺ a ∈ D f ∧ ∀ ϵ > 0 ∃ Δ > 0 ; ∀ x ∈ O ϵ ( a ) ; f ( x ) ∈ O ϵ ( f ( a ) ) \iff a \in D_f \land \forall \epsilon > 0 \, \exists \Delta > 0 ; \forall x \in O_{\epsilon}(a); f(x) \in O_{\epsilon}(f(a)) ⟺ a ∈ D f ∧ ∀ ϵ > 0 ∃Δ > 0 ; ∀ x ∈ O ϵ ( a ) ; f ( x ) ∈ O ϵ ( f ( a ))
Funkce f ( x ) f(x) f ( x ) a ⟺ a ∈ D f ∧ ∀ ϵ ∈ R + ∃ Δ ∈ R + ∀ x ∈ < a ; a + Δ ) ; f ( x ) ∈ ( f ( a ) − ϵ ; f ( a ) + ϵ ) a \iff a \in D_f \land \forall \epsilon \in \R^+ \exists \Delta \in \R^+ \forall x \in <a;a + \Delta); f(x) \in (f(a) - \epsilon; f(a) + \epsilon) a ⟺ a ∈ D f ∧ ∀ ϵ ∈ R + ∃Δ ∈ R + ∀ x ∈< a ; a + Δ ) ; f ( x ) ∈ ( f ( a ) − ϵ ; f ( a ) + ϵ )
Funkce f ( x ) f(x) f ( x ) a ⟺ a ∈ D f ∧ ∀ ϵ ∈ R + ∃ Δ ∈ R + ∀ x ∈ ( a + Δ ; a > ; f ( x ) ∈ ( f ( a ) − ϵ ; f ( a ) + ϵ ) a \iff a \in D_f \land \forall \epsilon \in \R^+ \exists \Delta \in \R^+ \forall x \in (a + \Delta;a> ; f(x) \in (f(a) - \epsilon; f(a) + \epsilon) a ⟺ a ∈ D f ∧ ∀ ϵ ∈ R + ∃Δ ∈ R + ∀ x ∈ ( a + Δ ; a > ; f ( x ) ∈ ( f ( a ) − ϵ ; f ( a ) + ϵ )
Funkce f ( x ) f(x) f ( x ) ⟺ f ( x ) \iff f(x) ⟺ f ( x ) ( c ; d ) ∧ f ( x ) (c; d) \land f(x) ( c ; d ) ∧ f ( x ) c c c ∧ f ( x ) \land f(x) ∧ f ( x ) d d d
Asymptoty
Asymptota je přímka, ke které funkce f konverguje.
Bez směrnice
Je kolmá na osu X a rovnoběžná s osou Y
je jí předpis je X = k X = k X = k
Se směrnicí
Její předpis je y = k x + q y = kx + q y = k x + q k = lim x → ∞ = f ( x ) x k = \lim_{x \to \infty} = \frac{f(x)}{x} k = lim x → ∞ = x f ( x ) q = lim x → ∞ = f ( x ) − k x q = \lim_{x \to \infty} = f(x) - kx q = lim x → ∞ = f ( x ) − k x
Derivace
Derivace funkce se značí přidáním ' za označení funkce.
f ′ ( a ) = lim h → 0 f ( a + h ) − f ( a ) h = lim x → a f ( x ) − f ( a ) x − a f'(a) = \lim_{h \to 0} \frac{f(a + h) - f(a)}{h} = \lim_{x \to a} \frac{f(x) - f(a)}{x - a} f ′ ( a ) = h → 0 lim h f ( a + h ) − f ( a ) = x → a lim x − a f ( x ) − f ( a ) Vzorce pro derivování funkcí
( k . f ( x ) ) ′ = k . f ′ ( x ) (k . f(x))' = k . f'(x) ( k . f ( x ) ) ′ = k . f ′ ( x ) ( f ( x ) ± g ( x ) ) ′ = f ′ ( x ) ± g ′ ( x ) (f(x) \pm g(x))' = f'(x) \pm g'(x) ( f ( x ) ± g ( x ) ) ′ = f ′ ( x ) ± g ′ ( x ) ( f ( x ) . g ( x ) ) ′ = f ′ ( x ) g ( x ) + f ( x ) g ′ ( x ) (f(x).g(x))' = f'(x)g(x) + f(x)g'(x) ( f ( x ) . g ( x ) ) ′ = f ′ ( x ) g ( x ) + f ( x ) g ′ ( x ) ( f ( x ) g ( x ) ) ′ = f ′ ( x ) g ( x ) − f ( x ) g ′ ( x ) g 2 ( x ) \bigg( \frac{f(x)}{g(x)}\bigg) ' = \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} ( g ( x ) f ( x ) ) ′ = g 2 ( x ) f ′ ( x ) g ( x ) − f ( x ) g ′ ( x ) [ f ( g ( x ) ) ] ′ = f ′ ( g ( x ) ) . g ′ ( x ) [f(g(x))]' = f'(g(x)).g'(x) [ f ( g ( x )) ] ′ = f ′ ( g ( x )) . g ′ ( x ) f ( x ) g ( x ) = e g ( x ) ln f ( x ) f(x)^{g(x)} = e^{g(x) \ln {f(x)}} f ( x ) g ( x ) = e g ( x ) l n f ( x ) ( [ f ( x ) ] g ( x ) ) ′ = [ f ( x ) ] g ( x ) ( g ′ ( x ) ln ( f ( x ) ) + g ( x ) f ′ ( x ) f ′ ( x ) ) ([f(x)]^{g(x)})' = [f(x)]^{g(x)} \bigg( g'(x)\ln (f(x)) + g(x)\frac{f'(x)}{f'(x)} \bigg) ([ f ( x ) ] g ( x ) ) ′ = [ f ( x ) ] g ( x ) ( g ′ ( x ) ln ( f ( x )) + g ( x ) f ′ ( x ) f ′ ( x ) ) Derivace elementárních funkcí
c ′ = 0 c' = 0 c ′ = 0 c ∈ R c \in \R c ∈ R
( x m ) ′ = m x m − 1 (x^m)' = mx^{m-1} ( x m ) ′ = m x m − 1 x ≠ 0 ∧ m ∈ Z x \neq 0 \land m \in \Z x = 0 ∧ m ∈ Z
( a x ) ′ = a x ln a (a^x)' = a^x\ln a ( a x ) ′ = a x ln a x ∈ ( 0 ; ∞ ) ∧ a ∈ R + x \in (0; \infty) \land a \in \R^+ x ∈ ( 0 ; ∞ ) ∧ a ∈ R +
( e x ) ′ = e x (e^x)' = e^x ( e x ) ′ = e x x ∈ R x \in \R x ∈ R
( ln x ) ′ = 1 x (\ln x)' = \frac{1}{x} ( ln x ) ′ = x 1 x ∈ R + x \in \R^+ x ∈ R +
( log a x ) ′ = 1 x ln a (\log_a x)' = \frac{1}{x\ln a} ( log a x ) ′ = x l n a 1 x ∈ R + x \in \R^+ x ∈ R +
( sin x ) ′ = cos ( x ) (\sin x)' = \cos(x) ( sin x ) ′ = cos ( x ) x ∈ R x \in \R x ∈ R
( cos x ) ′ = − sin ( x ) (\cos x)' = -\sin(x) ( cos x ) ′ = − sin ( x ) x ∈ R x \in \R x ∈ R
( tg x ) ′ = 1 cos 2 x (\tg x)' = \frac{1}{\cos^2 x} ( tg x ) ′ = c o s 2 x 1 x ∈ R − { π 2 + k π } ∧ k ∈ Z x \in \R - \{ \frac{\pi}{2} + k\pi \} \land k \in \Z x ∈ R − { 2 π + kπ } ∧ k ∈ Z
( cot x ) ′ = − 1 sin 2 x (\cot x)' = -\frac{1}{\sin^2 x} ( cot x ) ′ = − s i n 2 x 1 x ∈ R − { k π } ∧ k ∈ Z x \in \R - \{ k\pi \} \land k \in \Z x ∈ R − { kπ } ∧ k ∈ Z
( sinh x ) ′ = cosh x (\sinh x)' = \cosh x ( sinh x ) ′ = cosh x x ∈ R x \in \R x ∈ R
( cosh x ) ′ = sinh x (\cosh x)' = \sinh x ( cosh x ) ′ = sinh x x ∈ R x \in \R x ∈ R
( tanh x ) ′ = 1 cosh 2 x (\tanh x)' = \frac{1}{\cosh^2 x} ( tanh x ) ′ = c o s h 2 x 1 x ∈ R x \in \R x ∈ R
( coth x ) ′ = − 1 sinh 2 x (\coth x)' = - \frac{1}{\sinh^2 x} ( coth x ) ′ = − s i n h 2 x 1 x ∈ R − { 0 } x \in \R - \{0\} x ∈ R − { 0 }
( arcsin x ) ′ = 1 1 + x 2 (\arcsin x)' = \frac{1}{\sqrt {1 + x^2}} ( arcsin x ) ′ = 1 + x 2 1 x ∈ ( − 1 ; 1 ) x \in (-1;1) x ∈ ( − 1 ; 1 )
( arccos x ) ′ = − 1 1 − x 2 (\arccos x)' = - \frac{1}{\sqrt {1 - x^2}} ( arccos x ) ′ = − 1 − x 2 1 x ∈ ( − 1 ; 1 ) x \in (-1;1) x ∈ ( − 1 ; 1 )
( arctan x ) ′ = − 1 1 + x 2 (\arctan x)' = -\frac{1}{1 + x^2} ( arctan x ) ′ = − 1 + x 2 1 x ∈ R − { π 2 + k π } ∧ k ∈ Z x \in \R - \{ \frac{\pi}{2} + k\pi \} \land k \in \Z x ∈ R − { 2 π + kπ } ∧ k ∈ Z
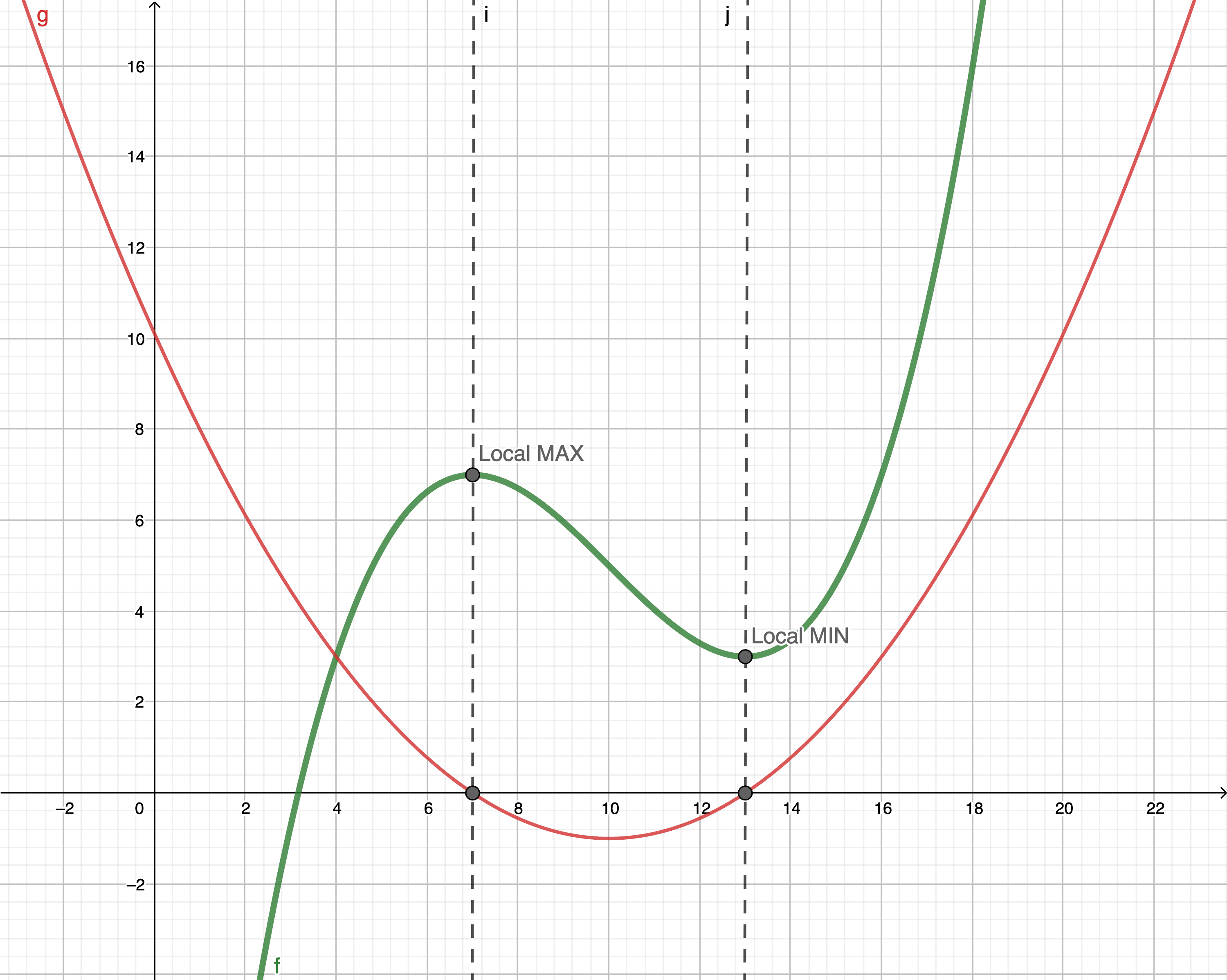
Stacionární body
Body ve kterých může funkce dosáhnout svého lokálního extrému.
V těchto bodech platí f ′ ( x ) = 0 f'(x) = 0 f ′ ( x ) = 0
Funkce f f f M ∈ D f M \in D_f M ∈ D f ⟺ ∃ U ; U = ( M − ϵ , M + ϵ ) ; ϵ > 0 ∧ ∀ x ∈ U ∩ D f \iff \exists U; U = (M - \epsilon,M + \epsilon); \epsilon > 0 \land \forall x \in U \cap D_f ⟺ ∃ U ; U = ( M − ϵ , M + ϵ ) ; ϵ > 0 ∧ ∀ x ∈ U ∩ D f f ( x ) ≤ f ( M ) f(x) \leq f(M) f ( x ) ≤ f ( M )
Funkce f f f M ∈ D f M \in D_f M ∈ D f ⟺ ∃ U ; U = ( M − ϵ , M + ϵ ) ; ϵ > 0 ∧ ∀ x ∈ U ∩ D f \iff \exists U; U = (M - \epsilon,M + \epsilon); \epsilon > 0 \land \forall x \in U \cap D_f ⟺ ∃ U ; U = ( M − ϵ , M + ϵ ) ; ϵ > 0 ∧ ∀ x ∈ U ∩ D f f ( x ) ≥ f ( M ) f(x) \geq f(M) f ( x ) ≥ f ( M )
Legenda:
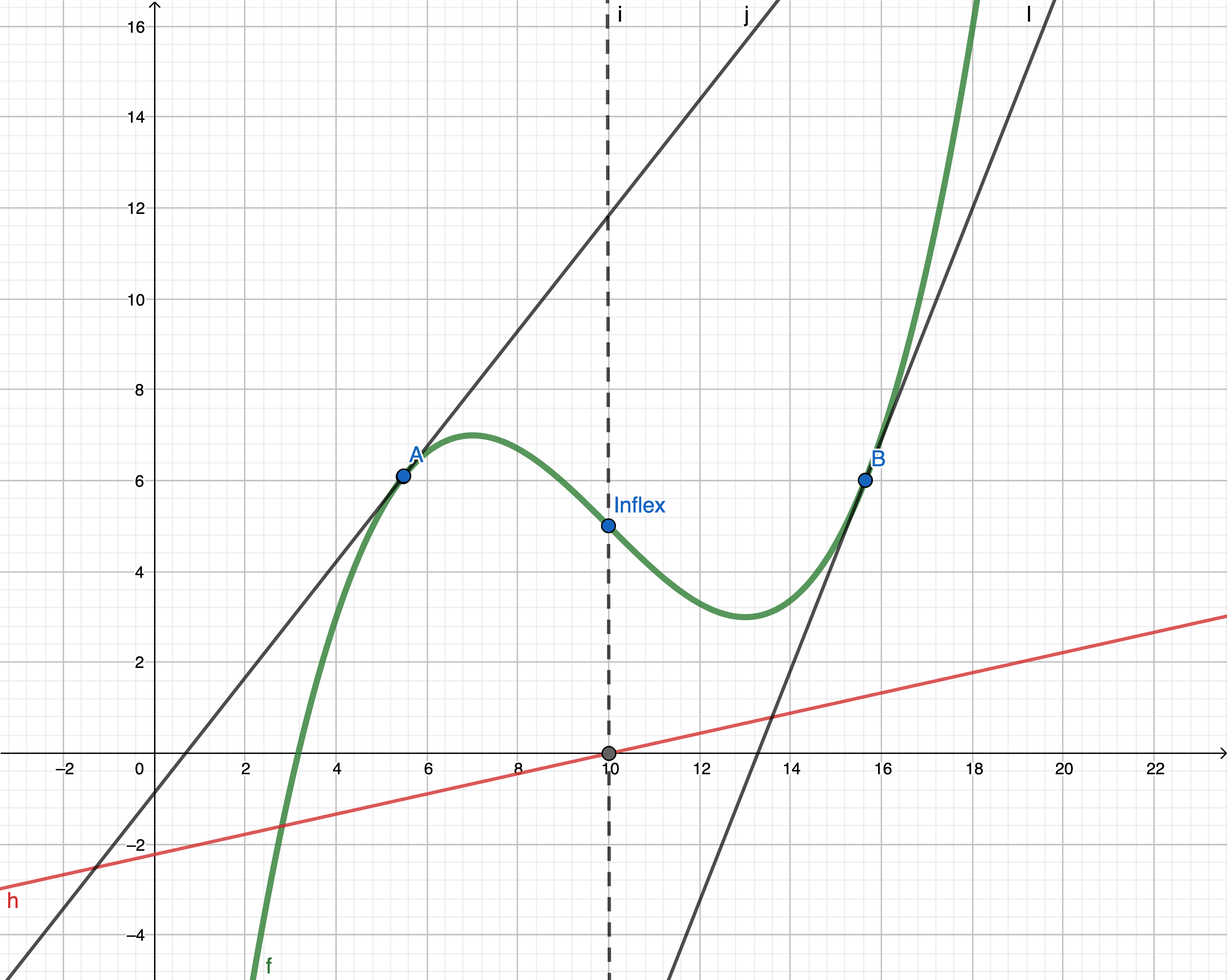
f : y = ( x − 10 3 ) 3 − ( x − 10 ) + 5 f: y = \bigg(\frac{x - 10}{3}\bigg)^3 - (x - 10) + 5 f : y = ( 3 x − 10 ) 3 − ( x − 10 ) + 5 g : f ′ ( x ) g: f'(x) g : f ′ ( x )
Monotónost
Funkce f f f ( A ; B ) (A;B) ( A ; B )
rostoucí ⟺ \iff ⟺ ∀ x ∈ ( A ; B ) ; f ′ ( x ) > 0 \forall x \in (A;B); f'(x) > 0 ∀ x ∈ ( A ; B ) ; f ′ ( x ) > 0
klesající ⟺ \iff ⟺ ∀ x ∈ ( A ; B ) ; f ′ ( x ) < 0 \forall x \in (A;B); f'(x) < 0 ∀ x ∈ ( A ; B ) ; f ′ ( x ) < 0
konstatní ⟺ \iff ⟺ ∀ x ∈ ( A ; B ) ; f ′ ( x ) = 0 \forall x \in (A;B); f'(x) = 0 ∀ x ∈ ( A ; B ) ; f ′ ( x ) = 0
neklesající ⟺ \iff ⟺ ∀ x ∈ ( A ; B ) ; f ′ ( x ) ≥ 0 \forall x \in (A;B); f'(x) \geq 0 ∀ x ∈ ( A ; B ) ; f ′ ( x ) ≥ 0
neroustoucí ⟺ \iff ⟺ ∀ x ∈ ( A ; B ) ; f ′ ( x ) ≤ 0 \forall x \in (A;B); f'(x) \leq 0 ∀ x ∈ ( A ; B ) ; f ′ ( x ) ≤ 0
Tečna ke grafu funkce
Tečna ke grafu funkce f f f T = [ x 0 , y 0 ] T = [x_0, y_0] T = [ x 0 , y 0 ] y 0 = f ( x 0 ) y_0 = f(x_0) y 0 = f ( x 0 )
y − y 0 = f ′ ( x 0 ) . ( x − x 0 ) y - y_0 = f'(x_0).(x - x_0) y − y 0 = f ′ ( x 0 ) . ( x − x 0 ) Inflexe
Pro bod podezřelý z inflexe platí: f ′ ′ ( x ) = 0 f''(x) = 0 f ′′ ( x ) = 0
Nechť J J J f f f J ⊂ D f J \subset D_f J ⊂ D f f f f
Konvexní na J ⟺ ∀ x , y ∈ J ∀ λ ∈ [ 0 , 1 ] : f ( λ x + ( 1 − λ ) y ) ≤ λ f ( x ) + ( 1 − λ ) f ( y ) J \iff \forall x,y \in J \forall \lambda \in [0,1]: f(\lambda x + ( 1 - \lambda )y) \leq \lambda f(x) + (1 - \lambda)f(y) J ⟺ ∀ x , y ∈ J ∀ λ ∈ [ 0 , 1 ] : f ( λ x + ( 1 − λ ) y ) ≤ λ f ( x ) + ( 1 − λ ) f ( y )
Konkávní na J ⟺ ∀ x , y ∈ J ∀ λ ∈ [ 0 , 1 ] : f ( λ x + ( 1 − λ ) y ) ≥ λ f ( x ) + ( 1 − λ ) f ( y ) J \iff \forall x,y \in J \forall \lambda \in [0,1]: f(\lambda x + ( 1 - \lambda )y) \geq \lambda f(x) + (1 - \lambda)f(y) J ⟺ ∀ x , y ∈ J ∀ λ ∈ [ 0 , 1 ] : f ( λ x + ( 1 − λ ) y ) ≥ λ f ( x ) + ( 1 − λ ) f ( y )
funkce f f f A A A ⟺ f ′ ′ ( A X ) > 0 \iff f''(A_X) > 0 ⟺ f ′′ ( A X ) > 0
funkce f f f A A A ⟺ f ′ ′ ( A X ) < 0 \iff f''(A_X) < 0 ⟺ f ′′ ( A X ) < 0
Legenda:
f : y = ( x − 10 3 ) 3 − ( x − 10 ) + 5 f: y = \bigg(\frac{x - 10}{3}\bigg)^3 - (x - 10) + 5 f : y = ( 3 x − 10 ) 3 − ( x − 10 ) + 5 g : f ′ ′ ( x ) g: f''(x) g : f ′′ ( x ) V bodě A A A
V bodě B B B
L’ Hospitalovo pravidlo
Nechť a ∈ R ∪ { − ∞ } , f , g a \in \R \cup \{-\infty\}, f,g a ∈ R ∪ { − ∞ } , f , g lim x → a + f ′ ( x ) g ′ ( x ) \lim_{x \to a^+} \frac{f'(x)}{g'(x)} lim x → a + g ′ ( x ) f ′ ( x ) lim x → a + f ( x ) = lim x → a + g ( x ) = 0 \lim_{x \to a^+} f(x) = \lim_{x \to a^+} g(x) = 0 lim x → a + f ( x ) = lim x → a + g ( x ) = 0 lim x → a + ∣ g ( x ) ∣ = ∞ \lim_{x \to a^+} |g(x)| = \infty lim x → a + ∣ g ( x ) ∣ = ∞ lim x → a + f ( x ) g ( x ) = lim x → a + f ′ ( x ) g ′ ( x ) \lim_{x \to a^+} \frac{f(x)}{g(x)} = \lim_{x \to a^+} \frac{f'(x)}{g'(x)} lim x → a + g ( x ) f ( x ) = lim x → a + g ′ ( x ) f ′ ( x )
Vyšetření průběhu funkce
Spojitost Sudost/lichost Průsečíky s osami První derivace
Stacionární body
Monotónost funkce
Lokální extrémy
Druhá derivace
Inflexní body
Konkávnost/konvexnost
Asymptoty
Asymptoty se bez směrnice
Asymptoty se směrnicí
Periodicita Funkční hodnoty ve význačných bodech Náčrt grafu Obor funkčních hodnot
Integrál
Primitivní funkce
Primitivní funkce se značí velkým písmenem. První derivace primitivní funkkce je funkce zadaná
F ′ ( x ) = f ( x ) F'(x) = f(x) F ′ ( x ) = f ( x ) Neurčitý integrál
Pro neurčitý integrál platí:
∫ k d x = k x + C \int k dx = kx + C ∫ k d x = k x + C
∫ x a d x = x a + 1 a + 1 + C \int x^a dx = \frac{x^{a + 1}}{a + 1} + C ∫ x a d x = a + 1 x a + 1 + C a ≠ − 1 a \neq -1 a = − 1
∫ e x d x = e x + C \int e^x dx = e^x + C ∫ e x d x = e x + C
∫ 1 x d x = ln ∣ x ∣ + C \int \frac{1}{x} dx = \ln ∣x∣ + C ∫ x 1 d x = ln ∣ x ∣ + C
∫ a x d x = a x ln a + C \int a^x dx = \frac{a^x}{\ln a} + C ∫ a x d x = l n a a x + C
∫ sin x d x = − cos x + C \int \sin x dx = -\cos x + C ∫ sin x d x = − cos x + C
∫ cos x d x = sin x + C \int \cos x dx = \sin x + C ∫ cos x d x = sin x + C
Integrace per partes
∫ u . v ′ = u . v − ∫ u ′ . v \int u.v' = u.v - \int u'.v ∫ u . v ′ = u . v − ∫ u ′ . v Integrace substitucí
∫ f ( ϕ ( t ) ) ⋅ ϕ ′ ( t ) d t = F ( ϕ ( t ) ) \int f(\phi (t)) \cdot \phi^{\prime}(t) dt = F(\phi(t)) ∫ f ( ϕ ( t )) ⋅ ϕ ′ ( t ) d t = F ( ϕ ( t )) s u b : x = ϕ ( t ) sub: x = \phi(t) s u b : x = ϕ ( t ) ∫ f ( ϕ ( t ) ) ⋅ ϕ ′ ( t ) d t = ∫ f ( x ) ⋅ x ′ d x = F ( x ) \int f(\phi(t))\cdot\phi^{\prime}(t) dt = \int f(x) \cdot x^{\prime} dx = F(x) ∫ f ( ϕ ( t )) ⋅ ϕ ′ ( t ) d t = ∫ f ( x ) ⋅ x ′ d x = F ( x ) Newton Leibnizova věta
∫ a b f ( x ) d x = [ F ( x ) ] a b = F ( b ) − F ( a ) \int_a^b f(x) dx = [F(x)]_a^b = F(b) - F(a) ∫ a b f ( x ) d x = [ F ( x ) ] a b = F ( b ) − F ( a ) Obsah pod grafem
Obsah útvaru ohraničeného grafem, osou X a dvěmi rovnoběžkami procházející hranicemi intervalu na které je útvar určen se rovná
∫ a b f ( x ) d x \int_a^b f(x) dx ∫ a b f ( x ) d x Objem rotačního tělesa
Objem rotačního tělesa lze vyjárřit jako
V = π ∫ a b f 2 ( x ) d x V = \pi \int_a^b f^2(x) dx V = π ∫ a b f 2 ( x ) d x