MATFYZ

Lineární algebra II

March 08 2022 [Edit]

Pokud naleznete nějakou chybu, můžete jí opravit pomocí tlačítka edit.

Shout out Míše Loudové za použití těchto poznámek jako zdroj do své bakalářské práce.

• Skalární součin
  • Komplexně sdružené číslo
  • Skalární součin nad $\R$
  • Skalární součin nad $\C$
  • Jednoznačnost obrazů báze vzhledem ke skalárnímu součinu
    • Známé normy
• Ortogonální a ortonormální systémy
  • Fourierovy koeficienty
  • Gramova-Schmitzova ortogonalizace
    • Příklad projekce na přímku při standardním skalárním součinu
  • Metoda nejmenších čtverců
    • Příklady ortogonálních matic
    • Givensova matice
• Determinant
  • Determinant horní trojúhelníkové matice
  • Determinant transpozice
  • Vlastnosti determinantů
  • Determinantská složitost
• Vlastní čísla
• Diagonalizovatelnost
  • Vlastnosti diagonalizovatelných matic
    • Příklad matice v Jordanově normální formě
    • Příklad mocninné matice
• Positivně (semi-)definitní matice

Skalární součin

Definice

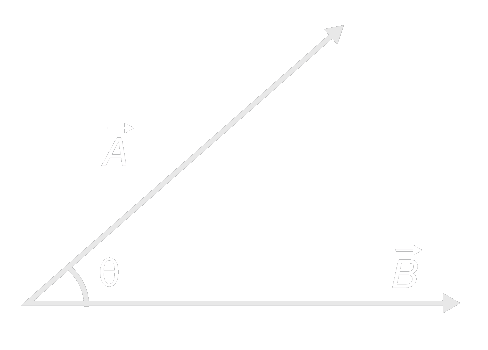
Standardní skalární součin $x,y \in \R^{n}$ je definován jako

$$x^{T}y = \sum_{i=1}^{n} x_{i}y_{i}$$

Geometrické vyjádření:

$$X^{T}Y = \| x \| . \| y \| . \cos(\phi)$$

Kdy $\phi$ je úhel svírající vektory $x$ a $y$.

Vlastnosti:

• $X^TX = \sum_{i=1}^n \geq 0$$$
• velikost vektoru $\left\| \vec{x} \right\| = \sqrt{x^Tx}$
• symetrie $x^Ty = y^Tx$
• lineární po složkách $(x + x')^Ty = x^Ty + x'^Ty$ a $(\alpha x)^Ty = \alpha(x^Ty)$ ale neplatí $(x + x')^T(y+y') \neq x^Ty + x'^Ty'$

V prostoru $\R^{m \times n}$ :

$$\langle A,B \rangle = \sum_{i = 1}^{m} \sum_{j = 1}^{n} a_{ij}b_{ij} = \text{trace}(AB^T)$$

Komplexně sdružené číslo

Komplexně sdružené číslo k číslu $a+bi$ je $\overline{a+bi} = a - bi$

Skalární součin nad $\R$

Buď $V$ je vektorový prostor nad $\R$. Pak skalární součin je zobrazení $\langle\ \cdot , \cdot \rangle : V^2 \rightarrow \R$, splňující pro všechna $x,y,z \in V$ a $\alpha \in \R$:

• $\langle x,x \rangle \geq 0$ a rovnost nastane pouze pro $x = 0$
• $\langle x+y,z \rangle = \langle x,z \rangle + \langle y,z \rangle$$$
• $\langle \alpha x,y \rangle = \alpha \langle x,y \rangle$$$
• $\langle x,y \rangle = \langle y,x \rangle$$$
  • $\langle x, \alpha y + \beta z \rangle = \alpha \langle x,y \rangle + \beta \langle x,z \rangle$$$

Skalární součin nad $\C$

Buď $V$ je vektorový prostor nad $\C$. Pak skalární součin je zobrazení $\langle\ \cdot , \cdot \rangle : V^2 \rightarrow \C$, splňující pro všechna $x,y,z \in V$ a $\alpha \in \C$:

• $\langle x,x \rangle \geq 0$ a rovnost nastane pouze pro $x = 0$
• $\langle x+y,z \rangle = \langle x,z \rangle + \langle y,z \rangle$$$
• $\langle \alpha x,y \rangle = \alpha \langle x,y \rangle$$$
• $\langle x,y \rangle = \overline{\langle y,x \rangle}$$$

Není lineární ve druhé složce.

Jednoznačnost obrazů báze vzhledem ke skalárnímu součinu

$B = \{ z_1, z_2, ... , z_n \}$ báze prostoru $V$ nad $\R$.
$x,y \in V$: $x = \sum_{i=1}^{n} \alpha_i z_i$ a $y = \sum_{j=1}^{n} \beta_j z_j$ pro určité $\{ \alpha_1,\alpha_2,...,\alpha_n \} \cup \{ \beta_1, \beta_2, ..., \beta_n \} \in \R$

$$\langle x,y \rangle = \left\langle \sum_{i=1}^{n} \alpha_i z_i , \sum_{j=1}^{n} \beta_j z_j \right\rangle = \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \beta_j \langle z_i,z_j \rangle$$

$\implies$ skalární součin je jednoznačně určený hodnotami součinů všech bazických vektorů.
(hodnoty si ale můžeme zvolit libovolně na rozdíl od lineárního zobrazení)

Definice

Norma indukovaná skalárním součinem

je definovaná:

$$\left\| x \right\| := \sqrt{\langle x,x \rangle} \text{ kde } x \in V$$

Pro normální skalární součin v $\R^n$: Euklidovská norma $\left\| x \right\| = \sqrt{\sum_{i=1}^n x_i^2}$

Definice

Kolmost

Vektory $x,y \in V$ jsou kolmé, tak

$$\langle x,y \rangle = 0$$

Značíme $x \perp y$

Věta

Pythagorova věta

Pokud $x,y \in V$ jsou kolmé, tak

$$\left\| x + y \right\|^2 = \left\| x \right\| ^2 = \left\| y \right\| ^2$$

Důkaz

$\left\| x + y \right\|^2 = \langle x+y,x+y \rangle = \langle x,x \rangle + \overbrace{\langle x,y \rangle}^{0} + \overbrace{\langle x,y \rangle}^{0} + \langle y,y \rangle = \langle x,x \rangle + \langle y,y \rangle = \left\| x \right\|^2 + \left\| x \right\|^2$

Věta

Couchyho-Schwartzova nerovnost

Pro každé $x,y \in V$ platí

$$\left\| \langle x,y \rangle \right\| \leq \left\| x \right\| . \left\| y \right\|$$

Důkaz

(reálná verze)

Pro $y=0$ platí zřejmě.
Předpokládejme, že $y \neq 0$ a funkci $f$, kdy $f(t) = \langle x + ty,x+ ty \rangle \geq 0$.

Pak

$$f(t) = \langle x,x \rangle + t\langle x,y \rangle + t\langle y,x \rangle + t^2\langle y,y \rangle = \\ \langle x,x \rangle + 2t\langle x,y \rangle + t^2\langle y,y \rangle$$

Funkce $f$ je všude nezáporná $\implies$ nemůže mít dva kořeny $\implies$ diskriminant je nekladný

$$D = 4t^2\langle x,y \rangle - 4t^2\langle x,x \rangle\langle y,y \rangle \leq \langle x,y^2 \rangle \langle x,x \rangle\langle y,y \rangle \leq 0$$ $$\Downarrow$$ $$\begin{align*} \langle x,y \rangle^{2} & \leq \langle x,x \rangle \langle y,y \rangle \\ \lvert x,y \rvert &\leq \| x \| \cdot \| y \| \end{align*}$$

Věta

Trojúhelníková nerovnost

Pro každé $x,y \in V$ platí:

$$\lVert x + y \rVert \leq \lVert x \rVert + \lVert y \rVert$$

Důkaz

$\lvert x + y \rvert ^2 =$
$\langle x + y, x + y \rangle =$
$\langle x,x \rangle~+~\langle y,y \rangle~+~\langle x,y \rangle~+~\langle y,x \rangle =$
$\langle x,x \rangle + \langle y,y \rangle + \overbrace{\langle x,y \rangle + \overline{\langle x,y \rangle}}^{2Re(\langle x,y \rangle)} =$
$\langle x,x, \rangle + 2Re(\langle x,y \rangle) \leq$
$\langle x,x \rangle + \langle y,y \rangle + 2\left\|\langle x,y \rangle \right\| \leq$
$\lvert x \rvert ^2 + \lvert y \rvert ^2 + 2\lvert x \rvert \cdot \lvert y \rvert =$
$\left( \lvert x \rvert . \lvert y \rvert \right)^2$

Definice

Buď $V$ vektorový prostor nad $\R$ nebo $\C$. Pak norma je zobrazeni $\|\cdot\|: V \rightarrow \R$ splňující:

1. $\left\| x \right\| \geq 0$ pro všechna $x \in V$, a rovnost pauze pro $x \neq 0$
2. $\left\|\alpha x\right\| = \left\| \alpha \right\| \cdot \left\|x\right\|$ pro všechna $x \in V$ a pro všechna $\alpha \in \R$ resp. $\alpha \in \C$
3. $\left\| x+y \right\| \leq \left\|x\right\| + \left\| y \right\|$$$

Tvrzení

Norma indukovaná skalárním součinem je normou.

Důkaz

1. z definice
2. $\left\| \alpha x \right\| = \sqrt{ \langle \alpha x, \alpha x \rangle} = \sqrt{ \alpha \overline{\alpha} \langle x,x \rangle} = \sqrt{ \alpha \overline{\alpha}} \sqrt{\langle x, x\rangle} = |\alpha| \cdot \|x\|$
3. vyplývá z trojúhelníkové nerovnosti

Lemma

Rovnoběžné pravidlo

Pro normu indukovanou skalárním součinem platí:

$$\| x - y \|^{2} + \| x + y \|^{2} = 2\| x \|^{2} + 2\| y \|^{2}$$

Definice

Metrika

Metriku na množině $M$ definujeme jako zobrazení $d: M^{2} \rightarrow \R$ splňující:

1. $d(x,y) \geq 0$, rovnost pouze pro $x=y$
2. $d(x,y) = d(y,x)$
3. $d(x,z) \leq d(x,y) + d(y,z)$

Poznámka

Každá norma určuje metriku předpisem:

$$d(x, y) := \left\| x-y \right\|$$

Tedy vzdálenost vektorů $x,y$ se zavádí jako velikost jejich rozdílů.

Definice

Pro $p=1,2,\ldots$ definujeme $p$-normu vektoru $x \in \R^{n}$ jako $\left\| x \right\|_{p} = \left(\sum_{i=1}^{n} \lvert x_{i} \rvert^p \right)^{\frac{1}{p}}$.

Známé normy

$p=1$	Součtová norma	$\left| x \right|_{1} = \sum^{n}_{i=1} \lvert x_{i} \rvert$
$p=2$	Euklidovská norma	$\left| x \right|_{2} = \sqrt{\sum^{n}_{i=1} x_{i}^{2}}$
$p=\infty$	Maximorá norma	$\left| x \right|_{\infty} = \max_{i=1,...,n} \lvert x_{i} \rvert$

---

Ortogonální a ortonormální systémy

Definice

Systém vektorů $z_{1}, \ldots, z_{n}$ je

• Ortogonální pokud je $\forall i,j: \langle z_{i},z_{j} \rangle = 0$
• Ortonormální pokud je ortogonální a $\forall i: \left\| z_{i} \right\| = 1$

• Je-li $z_{1},\ldots,z_{n}$ nenulové a ortogonální, pak $\frac{1}{\| z_{1} \|}z_{1}, \ldots, \frac{1}{\| z_{n} \|}z_{n}$ je ortonormální.
• Je-li systém ortogonální a neobsahuje nulový vektor, potom je také lineárně nezávislý.

Tvrzení

Je-li systém $z_{1}, \ldots, z_{n}$ ortonormální, pak je lineárně nezávislý.

Důkaz

$\langle\sum_{i=1}^{n} \alpha_{i} z_{i}, z_{k}\rangle = \langle 0, z_{k}\rangle = 0$
$\langle\sum_{i=1}^{n} \alpha_{i} z_{i}, z_{k}\rangle = \sum_{i=1}^{n} \alpha_{i} \langle z_{i}, z_{k} \rangle = 0$

Fourierovy koeficienty

Věta

Buď $z_{1}, \cdots, z_{n}$ ortonormální báze prostoru $V$. Pak pro každé $x \in V$ platí:

$$\underbrace{ x = \sum^{n}_{i=1}\hspace{-2em} \overbrace{\langle x, z_{i} \rangle}^{\text{Fourierovy~koeficienty\\}}\hspace{-2em} z_{i} }_{\text{Fourierův~rozvoj}}$$

Důkaz

$x = \sum^{n}_{i=1} \alpha_{i}z_{i} \rightarrow$ lineární kombinace
$\langle x, z_{k} \rangle = \sum^{n}_{i=1} \langle x, z_{i} \rangle z_{k} = \alpha_{k} \langle z_{k}, z_{k} \rangle = \alpha_{k}$$$

Představuje projekci na bazické vektory

Gramova-Schmitzova ortogonalizace

Algoritmus:
Vstup: lineárně nezávislé vektory $x_{1}, \ldots, x_{n} \in V$

1. for $k:=1$ to $n$
2. $\quad y_{k} := x_{k} - \sum^{k-1}_{j=1} \langle x_{k},z_{j} \rangle z_{j}$ // nakolmíme odečtením projekce do podprostoru
3. $\quad z_{k} := \frac{y_{k}}{\left\| y_{k} \right\|}$
4. end for

Výstup: $z_{1},\ldots, z_{n}$ ortonormální báze prostoru $span\{x_{1},\ldots,x_{n}\}$

Důkaz

Matematickou indukcí:

1. $n=1$$$
2. Indukční předpoklad: $z_{1}, \ldots, z_{n-1}$ je ortonormální bází $span\{x_{1},\ldots,x_{n-1}\}$, $y_{n}$ je nenulové z lineární nezávislosti, je dobře definovaná a má jednotkovou délku pak už jen dokážeme, že je kolmý a že tvoří bázi.

Tvrzení

Důsledek: Existence ortonormální báze

Každý konečně generovaný prostor se skalárním součinem má ortogonální bázi.

Důkaz

Každý má bázi a tu můžeme Gram-Schmitzem ortogonalizovat.

Tvrzení

Důsledek: Rozšíření ortonormálních systémů na ortonormální bázi

Každý ortonormální systém vektorů v konečně generovaném prostoru lze rozšířit na ortonormální bázi.

Věta

Buď $z_{1},\ldots,z_{n}$ ortonormální systém ve $V$ a buď $x \in V$.

Besselova nerovnost:

$$\| x \|^{2} \geq \sum^{n}_{j=1} \lvert \langle x_{j},z_{j} \rangle \rvert$$

Parsevalova rovnost:

$$\| x \|^{2} = \sum^{n}_{j=1} \lvert \langle x_{j},z_{j} \rangle \rvert \iff x \in span\{z_{1},\ldots, z_{n}\}$$

Tvrzení

Buď $B=\{z_{1},\ldots,z_{n}\}$ báze prostoru $V$. Pak

$$\langle x,y \rangle := [x]^{T}_{B} \overline{[y]}_{B}$$

Je skalárním součinem a báze $B$ je v něm ortonormální bází:

Důkaz

Stačí ověřit z definic:

1. $\langle x,x \rangle = [x]^{T}_{B}\overline{[x]}_{B} \geq 0$$$
2. linearita v první složce vyplývá z linearity souřadnic
3. symetrie také ze symetrie souřadnic

Příklad:
$A := _{B}[id]_{kan}$$$
$\langle x,y \rangle = [x]^{T}_{B}[y]_{B} = [x]^{T}_{kan} {\text{}}_{B}[id]^{T} {}_{B}[id] [y]_{kan} = x^{T}A^{T}A_{y}$

• $\langle \cdot , \cdot \rangle$ je skalární součin $\equiv$ je tvaru $\langle x,y \rangle = [x]^{T}_{B} \overline{[y]}_{B}$ pro nějakou ortogonální bázi $B$
• Každý skalární součin je standardní skalární součin při pohledu z libovolné ortonormální báze
• Analogicky pro normu:

$$\| x \| = \left\| [x]_{B} \right\|_{2} = \sqrt{[x]^{T}_{B}\overline{[x]}_{B}}$$

Definice

Definice ortogonální báze

Projekce vektoru $x \in V$ do podprostoru $U \Subset V$ je takový vektor $x_{_{U}} \in U$, který splňuje

$$\| x - x_{_{U}} \| = \min_{y \in U} \| x - y \|$$

Tvrzení

Tvrzení o kolmici

Buď $U \Subset V$, buď $x \in V$ a $y \in U$ takové, že $x-y \in U^{\perp}$. Pak

$$\| x - y \| < \| x - z \| \quad \forall z \in U \setminus \{y\}$$

Tedy vektor $y$ je jednoznačnou projekcí vektoru $x$ do $U$.

Důkaz

z předpokladu $(x-y)\perp(y-z)$
využitím Pythagorovy věty $\| x-z \|^{2} = \| x - y \|^{2} + \| y-z \|^{2} \geq \| x - y \|^{2}$
rovnost nastane jen pro $y=z$ protože $0$ je norma jen pro nulový vektor.

Věta

Buď $U \Subset V$. Pak pro každé $x \in V$ existuje právě jedna projekce $x_{_{U}} \in U$ do podprostoru $U$.

Navíc jeli $z_{1}, \ldots, z_{n}$ ortonormální báze $U$ pak

$$x_{_U} = \sum^{n}_{i=1} \langle x,z_{i} \rangle z_{i}$$

Důkaz

Rozšíříme bázi $U$ na bázi $V$ $z_{1},\ldots, z_{m}, z_{m+1},\ldots, z_{n}$
Definujeme $y = \sum^{m}_{i=1} \langle x,z_{i} \rangle z_{i} \in U$ a ukážeme, že je projekcí

$$x - y = \sum^{n}_{i=1} \langle x,z_{i} \rangle z_{i} - \sum^{m}_{i=1} \langle x,z_i \rangle z_i = \sum^{n}_{i=n+1} \left\langle x,z_{i} \right\rangle z_{i} \in U^{\perp}$$

Poznámka: Ortogonální projekce je lineární zobrazení

Definice

Buď $V$ vektorový prostor a $U$ jeho podprostor. Pak projekcí $x \in U$ rozumíme takový $x_{U} \in U$, který splňuje

$$\| x - x_{U} \| = \min_{y \in U} \| x -y \|$$

Důsledek

Vektor $y \in U$ je projekcí vektoru $x \in V$ do podprostoru $U$ právě tehdy, když $x-y \in U^{\perp}$

Věta

Věta o ortogonální projekci

Buď $U$ podprostor $V$. Pak pro $\forall x in V$ existuje právě jedna projekce $x_{0} \in U$ do $U$.

Navíc, je-li $z_{1},\ldots, z_{m}$ ortonormální báze $U$, pak

$$x_{_{U}} = \sum^{m}_{i=1} \langle x,z_{i} \rangle z_{i}$$

Důkaz

$$x-x_{_{U}} = \sum^{n}_{i=1} \langle x,z_{i} \rangle z_{i} - \sum^{m}_{i=1} \langle x,z_{i} \rangle z_{i} \in U^{\perp}$$

• $y \in U$$$
• $x-x_{_{U}} \in U^{\perp}$$$
• $x_{_{U}} - y \in U$$$

Tudíž $(x - x_{_{0}}) \perp (x_{_{U}} - y)$. Použijeme pythagorovu větu:

$$\| x + y \|^{2} = \|(x - x_{_{U}}) + (x_{_{U}} - y) \|^{2} = \| x - x_{_{U}} \|^{2} + \| x_{_{U}} - y \| \geq \| x_{_{u}} \|^{2}$$

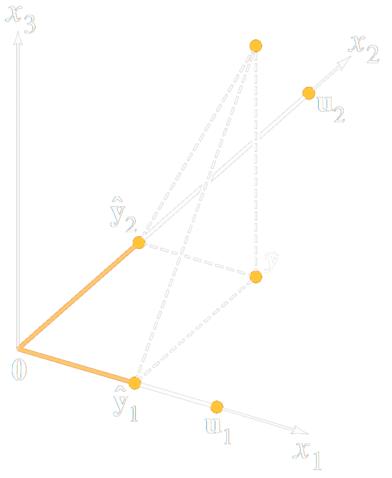
Příklad projekce na přímku při standardním skalárním součinu

• $a \in \R^{n}$ je nenulový vektor a uvažujeme projekci $x$ na přímku se směrnicí $a$ ($\implies$ do $span\{a\}$)
• Ortogonální báze $U = z = \frac{1}{\|a\|}a$

$$x_{u} = \langle x,z \rangle z = \frac{1}{\| a \|^{2}} \langle x,a \rangle a = \frac{x^{T}a}{a^{T}a}a$$

Tvrzení

Buď $B$ ortonormální báze prostoru $V$ se skalárním součinem. Pak

$$\langle x,y \rangle = [x]^{T}_{B}\overline{[y]}_{B} \quad \forall x,y \in V$$

Důkaz

Buď $B = \{ z_{1}, \ldots, z_{n}\}$. Pak $[x]_{B} = (\langle x, z_{1} \rangle, \ldots, \langle x, z_{n} \rangle)^{T}$

$$\langle x,y \rangle = \left\langle \sum^{n}_{j=1} \left\langle x,z_{j} \right\rangle z_{j}, y \right\rangle = \sum^{n}_{j=1} \langle x,z_{j} \rangle \overline{\langle y,z_{j} \rangle} = [x]^{T}_{B}\overline{[y]}_{B}$$

Definice

Buď $V$ vektorový prostor a $M \subseteq V$. Ortogonální doplněk množiny $M$ je

$$M^{\perp} := \{x \in V; \langle x,y \rangle = 0 \quad \forall y \in M \}$$

Ortogonální doplněk prostoru = ortogonální doplněk báze

Tvrzení

Buď $V$ vektorový prostor a $M,N \subseteq V$. Pak

1. $M^{\perp}$ je podprostor $V$
2. je-li $M \subseteq N$ pak $M^{\perp} \subseteq N^{\perp}$
3. $M^{\perp} = span(M)^{\perp}$$$

Důkaz

1. Ověřením vlastností podprostoru
2. Buď $x \in N^{\perp}$, tedy $\langle x,y \rangle = 0 \; \forall y \in N \langle x,y \rangle = 0 \; \forall y \in M \subseteq N$ a proto $x \in M^{\perp}$
3. $M \subseteq span(M)$ a dle 2. $M^{\perp} \subseteq span(M)^{\perp}$$$

Věta

Vlastnosti ortogonálního doplňku podprostoru

Buď $U \Subset V$, buď $z_{1},\ldots,z_{n}$ ortogonnální báze $V$, a buď $z_{1},\ldots, z_{n}, z_{n+1},\ldots, z_{m}$ její rozšíření na ortonormální bázi $V$. Pak $z_{n + 1}, \ldots, z_{m}$ je ortonormální báze $U^{\perp}$

Důkaz

Stačí dokázat $span\{z_{n+1},\ldots,z_m\} = U^{\perp}$.
Inkluze “$\supseteq$” vezmeme Fourierův rozvoj - prvních $m$ členů vypadne a zbude:

$$x = \sum^{m}_{i=n+1} \langle x,z \rangle z_{i} \in span\{z_{n + 1}, \ldots, z_{m}\}$$

Inkluze “$\subseteq$” Buď $x \in span\{z_{n+1},\ldots,z_{m}\}$

$$x = \sum^{m}_{i=n+1} \langle x,z \rangle z_{i} = \sum^{n}_{i=1} 0z_{i} + \sum^{m}_{i=n+1} \langle x,z_i \rangle z_{i}$$

Věta

Důsledek: Vlastnosti ortogonálního doplňku podprostoru

Buď $U \Subset V$. Potom platí

1. $\dim V = \dim U + \dim U^{\perp}$$$
2. $V = U + U^{\perp}$$$
3. $U \cap U^{\perp} = \{0\}$$$
4. $U = (U^{\perp})^{\perp}$$$
5. Je-li $z_{1},\ldots,z_{m}$ ortonormální báze $U$, a je-li $z_{1},\ldots,z_{m}, z_{m+1},\ldots, z_{n}$ její rozšíření na ortonormální bází $V$, pak $z_{m+1},\ldots,z_{n}$ je ortonormální báze $U^{\perp}$.

Důkaz

2. $dim V = n$,$dim U = m$, $dim U^{\perp} = n - m$
5. $z_{m+1},\ldots,z_{n}$ je ortonormální systém. Chceme dokázat, že $span\{z_{m+1},\ldots,z_{n}\} = U^{\perp}$A

$$\forall x \in V: x = \sum^{n}_{i=1} \langle x,z_{i} \rangle z_{i}$$

Je-li $x \in U^{\perp}$, pak $\langle x,z_{i} \rangle = 0, \; i = 1 \ldots m$ a tudíž

$$x = \sum^{n}_{i=m+1} \langle x,z_{i} \rangle z_{i} \in span\{z_{m+1},\ldots,z_{n}\}$$

Věta

Buď $A \in \R^{m \times n}$. Pak $R(A)^{\perp} = Ker(A)$

Důkaz

$R(A)^{\perp} = \left\{ \left( A_{1~*} \right)^{T}, \ldots \left( A_{m~*} \right)^{T}\right\}$
Tedy $x \in R(A)^{\perp} \equiv x \perp$ na řádky $A$

Důsledek

Buď $A \in \R^{m \times n}$. Pak $R(A) \oplus Ker(A) = \R^{n}$

Věta

Větička o vlastnostech matice $A$ versus $A^{T}A$

Buď $A \in \R^{m \times n}$. Pak

1. $Ker(A^{T}A) = Ker(A)$$$
2. $R(A^{T}A) = R(A)$$$
3. $rank(A^{T}A) = rank(A)$$$

Důkaz

1. Je-li $x \in Ker(A)$, pak $Ax = 0$ a tedy

$$A^{T}Ax = A^{T}0 = 0 \implies x \in Ker(A^{T}A)$$

obráceně

$$x \in Ker(A^{T}A) \rightarrow x^{T}A^{T}Ax = 0 \rightarrow (Ax)^{T}Ax = 0 \rightarrow (Ax)^{2} = 0$$

2. vyřešíme $R(A) = ker(A)^{\perp}$
3. Když jsou stejné řádky, potom mají stejnou dimenzi a i hodnost

Tvrzení

Maticové prostory a lineární zobrazení

Uvažujme lineární zobrazení $f(x)=Ax$, kde $A \in \R^{m \times n}$. Pokud definiční obor $f(x)$ omezíme pouze na prostor $R(A)$, dostaneme isomorfismus mezi $R(A)$ a $f(\R^{n})$.

Důkaz

Buď $x \in \R^{n}, R(A) \oplus Ker(A) = \R^{n}$, rozložíme na $x=x_{r}+x_{k}$, kde $x_{r} \in R(A)$ a $x_{k} \in Ker(A)$. Pak

$$f(x) = Ax = A(x_{r} + x_{k}) = Ax_r + \overbrace{Ax_{k}}^{0} = Ax_{r}$$

Věta

Buď $A \in \R^{m \times n}$ hodností $n$. Pak je projekce vektoru $x \in \R^{m}$ do sloupcového prostoru $S(A)$

$$x' = A(A^{T}A)^{-1}A^{T}x$$

Důkaz

Nejdříve dokážeme, že je dobře definován, pak $x' \in S(A)$ a $x - x' \in S(A)^{\perp}$
$x' \in S(A)$, $x' = Az$ pro $z = \left(A^{T}A\right)^{-1}A^{T}x$
$x-x' \in S(A)^{\perp} = R(A^{T})^{\perp} = Ker(A^{T}) \rightarrow$ vynásobíme s $A^{T}(x - x') = 0$ (po úpravě)

Definice

Matice projekce do $S(A)$

$$P := A(A^{T}A)^{-1}A^{T} ( = AA^{T} \text{ pro ortonormální bázi})$$

• $P$ je symetrická
• platí $P^2 = P$
• $S(P) = S(A) \rightarrow rank(P) = rank(A)$$$

Tvrzení

Matice $P \in \R^{n \times n}$ je maticí projekce právě tehdy když je symetrická a $P = P^2$.

Příklad:
Matice projekce $P = a(a^{T}a)^{-1}a^{T}$

$$Px = a(a^{T}a)^{-1}a^{T}x = \frac{a^{T}x}{a^{T}a}a$$

pokud $a$ znormujeme, tak $P = aa^{T}$.

Věta

Ortogonální projekce do doplňku

Buď $P \in \R^{n \times n}$ matice projekce do podprostoru $V \Subset \R^{n}$. Pak $I - P$ je maticí projekce do $V^{\perp}$

Důkaz

$\forall x \in \R^{n}$ platí $x = y + z$ kde $y \in V$ a $z \in V^{\perp}$.
Zde $y$ je projekce $x$ do $V$ a $z$ projekce $x$ do $V^{\perp}$

Metoda nejmenších čtverců

$$\min_{x \in \R^{n}} \left\| Ax - b \right\|^{2}_{2} = \min_{x \in \R^{n}} \sum^{n}_{i=1} \left( A_{i~*}x - b_{i} \right)^{2}$$

přenásobíme $A^{T}$

$$A^{T}Ax = A^{T}b$$

Věta

Množina přibližných řešení soustavy $Ax=b$ metodou nejmenších čtverců je neprázdná a rovna množině řešení normálních rovnic.

Důkaz

Hledáme projekci $b$ do podprostoru $S(A)$.
Projekce je tvaru $Ax$, kde $x \in \R^{n}$.
Víme, že $Ax$ je projekcí $\equiv Ax-b \in S(A)^{T} - Ker(A)^{T}$
$\implies A^{T}(Ax - b) = 0 \implies A^{T}Ax = A^{T}b$.

Důsledek

Buď $A \in R^{m \times n}$ hodnosti $n$. Pak přibližné řešení soustavy $Ax=b$ metodou nejmenších čtverců je jednoznačné a tvaru

$$x^{*} = (A^{T}A)^{-1}A^{T}b$$

Definice

Matice $Q \in \R^{n}$ je ortogonální pokud $Q^{T}Q = I_{n}$ ($Q^{-1} = Q^{T})$
Matice $Q \in \R^{n}$ je unitární, pokud $\overline{Q^{T}}Q = I_{n}$

Tvrzení

Charakterizace ortogonálních matic

Matice $Q \in \R^{n \times n}$ je ortogonální právě tehdy když sloupce $Q$ tvoří ortonormální bázi $\R^{n}$.

Důkaz

$$(Q^{T}Q)_{ij} = \langle Q_{*i}, Q_{*j} \rangle = \begin{cases} 1 & i = j\\ 0 & i \neq j \end{cases}$$

Tvrzení

Buď $Q \in \R^{n \times n}$ ortogonální. Pak

1. $Q^{T}$ je ortogonální
2. $Q^{-1}$ existuje a je ortogonální

Tvrzení

Součin ortogonálních matic

Jsou-li $Q_{1},Q_{2} \in \R^{n \times n}$ ortogonální, pak $Q_{1}Q_{2}$ je taky ortogonální.

Důkaz

$$(Q_{1}Q_{2})^{T}(Q_{1}Q_{2}) = Q^{T}_{2}Q^{T}_{1}Q_{1}Q_{2} = Q^{T}_{2}Q_{2} = I_{n}$$

Příklady ortogonálních matic

• $I_{n}$ a k ní opačná $-I_{n}$
• Housenholderova matice: $H(a) := I_{n} - \frac{2}{a^{T}a}$, kde $0 \neq a \in \R^{n}$ (zrcadlení dle nadroviny)
• Givensova matice: matice otáčení v rovině dvou os
• Matice otáčení kolem osy $2\frac{aa^{T}}{a^{T}a} - I_{n}$

Poznámka

každou ortogonální matici řádu $n$ lze vyjádřit jako součin maximálně $n$ Hesenholderových matic

Givensova matice

pro $n=2$

$$\begin{pmatrix} \cos \phi & -\sin \phi \\ \sin \phi & cos \phi \end{pmatrix}$$

otočí $\phi$ protisměru hodinových ručiček, kde $\cos^{2} \phi + \sin^{2} \phi = 1$. Pro větší $n$ doplňujeme jednotkovými maticemi.

Poznámka

Každou ortogonální matici řádu $n$ lze vyjádřit jako součin max $\binom{n}{2}$ Givensových matic.

Věta

Buď $Q \in \R^{n \times n}$ ortogonální. Pak

1. $\langle Qx,Qy \rangle = \langle x,y \rangle$ pro každé $x,y \in \R^{n}$
2. $\| Qx \| = \| x \|$ pro každé $x \in \R^{n}$ (kdy i rozšířená matice o 1 řád je ortogonální)

Důkaz

1. $\langle Qx Qy \rangle = \left( Qx \right)^{T} Qy - x^{T}Q^{T}Qy = x^{T}I_{n}y = x^{T} = \langle x,y \rangle$$$
2. $\| Q_{x} \| = \sqrt{\left\langle Qx, Qx \right\rangle} - \sqrt{\left\langle x,x \right\rangle} = \|x\|$$$

$\implies$ zobrazení $x \rightarrow Qx$ zachová úhly a délky jen pro ortogonální matice

Věta

Buď $Q \in \R^{n \times n}$ ortogonální. Pak

1. $\lvert Q_{ij} \rvert \leq 1$ a $\lvert Q^{-1}_{ij} \rvert \leq 1$ pro každé $i,j=1,\ldots,n$
2. $\begin{pmatrix} 1 & 0 \\ 0 & Q \end{pmatrix}^{T}$ je ortogonální amtice

Důkaz

Buď $z_{1},\ldots,z_{n}$ báze $\R^{n}$, buď $v \in \R^{n}$ a chceme $v=\sum^{n}_{i=1} x_{i}z_{i}$

Determinant

Definice

Determinant zobrazení $\lvert A \rvert$

$$\det(A) = \sum_{\Pi \in S_{n}} sgn(\Pi) \prod^{n}_{i=1} a_{i~\Pi_{\left( i \right)}}$$

Celkový počet permutací je $n!$

Determinant horní trojúhelníkové matice

$A \in \Pi^{n \times n}$ je horní trojúhelníková matice. Pak

$$\det(A) = a_{1~1} \cdot a_{2~2} \cdot \ldots \cdot a_{n~n}$$

Determinant transpozice

$$\det(A^T) = \sum_{\Pi \in S_{n}} sgn(\Pi) \prod^{n}_{i=1} a_{i~\Pi_{\left( i \right)}} = \det(A)$$

Vlastnosti determinantů

• $\det(A \cdot B) = \det(A) \cdot \det(B)$$$
• $\det(A^{-1}) = det(A)^{-1}$$$

Determinantská složitost

Věta

Řádková linearita determinantu $A \in \Pi^{n \times n}, b \in \Pi^{n}$. Potom pro každé $i \leq n$ platí, že

$$\det(A + eb^{T}) = \det(A) + \det(A + e \cdot (b^{T} - A_{i~*}))$$

Věta

Výpočet determinantu pomocí Gaussovy eliminace

• Vynásobení $i$-tého řádku $\alpha \in \Pi$

$$\det(A') = \alpha\det(A)$$

• Výměna $i$-tého a $j$-tého řádku

$$\det(A') = -\det(A)$$

• Přičtení $\alpha$ násobku $j$-tého řádku

$$\det(A') = \det(A)$$

Důsledek:
Matice $A$ je regulární právě tehdy když $\det(A) \neq 0$

Věta

Laplacův rozvoj podle $i$-tého řádku $A \in \Pi^{n \times n}$ $n \geq 2$, pro každé $i=1,\ldots,n$

$$\det(A) = \sum^{n}_{j=1} (-1)^{i+j}a_{i~j} \det(A^{ij})$$

Věta

$A \in \Pi^{n \times n}$ regulární, $b \in \Pi^{n}$

$$x_{i} = \frac{\det(A + ( b - A_{*~i})e_{i}}{\det(A)}~;~i=1,\ldots,n$$

Důsledek

Zobrazení $(A,b) \rightarrow A^{-1}b$ je spojité na definičním oboru regulárních matic.

Věta

Gaussovu eliminaci lze provádět tak, že k zápisu každé matice během výpočtu stačí pouze polynomiální počet bitů (v $k$).

Definice

Adjungovaná matice

Nechť $A \in \Pi^{n \times n}, n \geq 2$.

$$adj(A)_{i~j} = (-1)^{i = j}\det(A^{j~i})~;~i,j = 1,\ldots,n$$

kde $A^{ji}$ vznikne z $A$ vynecháním $j$-tého řádku a $i$-tého sloupce.

Věta

$$A \Subset \Pi^{n \times n} \implies A adj(A) = \det(AI_{n})$$

Důsledek

$A \in \Pi^{n \times n}$ je regulární. Potom $A^{-1} = \frac{1}{\det(A)}adj(A)$

Vlastní čísla

Definice

Vlastní čísla a vlastní vektory

Buď $A \in \C^{n \times n}$. Pak $\lambda \in \C$ je vlastní číslo matice $A$ a $x \in \C^{n}$ jemu příslušný vlastní vektor pokud

$$Ax = \lambda x \land x \neq 0$$

Věta

Buď $A \in \C^{n \times n}$. Pak

1. $\lambda \in \C$ je vlastním číslem $A$ právě tehdy když

$$\det(A - \lambda I_{n}) = 0$$

2. $x \in \C^{n}$ je příslušným vlastním vektorem právě tehdy, když

$$0 \neq x \in Ker(A -\lambda I_{n})$$

Tvrzení

Vlastní čísla trojúhelníkové matice

Nechť $A \in \C^{n \times n}$ je trojúhelníková matice. Pak její vlastní čísla jsou prvky na diagonále.

Definice

Charakteristický polynom matice $A \in \C^{n \times n}$ proměnné $\lambda$ je

$$P_{A} = \det(A -\lambda I)$$

Věta

Vlastní čísla matice $A \in \C^{n \times n}$ jsou právě kořeny jejího charakteristického polynomu $P_{A}(\lambda)$ a je jich $n$ včetně násobností.

Definice

Buď $\lambda \in \C$ vlastní číslo matice $A \in \C^{n \times n}$.

1. Algebraická násobnost $\lambda$ je rovna
2. Geometrická násobnost $\lambda$ je rovna $n - rank(A-\lambda I_{n})$, to je počtu lineárně nezávislých vlastních vektorů, které odpovídají $\lambda$.

Tvrzení

Součin a součet vlastních čísel:

1. $\det(A) = \lambda_{1} \cdot \ldots \cdot \lambda_{n}$$$
2. $trace(A) = \lambda_{1} + \ldots + \lambda_{n}$$$

A je regulární právě tehdy když $0$ není její vlastní číslo.

Tvrzení

Nechť $A \in \C^{n \times n}$ má vlastní čísla $\lambda_{1}, \ldots, \lambda$ a jim odpovídající vlastní vektory $x_{1}, \ldots, x_{n}$. Pak

1. je-li $A$ regulární, pak A^{-1} má vlastní čísla $\lambda^{-1}_{1}, \ldots \lambda^{-1}_{n}$ a vlastní vektory $x_{1}, \ldots, x_{n}$
2. $A^{2}$ má vlastní čísla $\lambda^{2}_{1}, \ldots, \lambda^{2}_{n}$ a vlastní vektory $x_{1}, \ldots, x_{n}$
3. $\alpha A$ má vlastní čísla $\alpha \lambda, \ldots, \alpha \lambda_{n}$ a vlastní vektory $x_{1}, \ldots, x_{n}$
4. $A + \alpha I_{n}$ má vlastní čísla $\lambda_{1} + \alpha, \ldots, \lambda_{n}+ \alpha$ a $x_{1}, \ldots, x_{n}$
5. $A^{T}$ má vlastní čísla $\lambda_{1}, \ldots, \ldots_{n}$, ale vlastní vektory obecně jiné.

Je-li $\lambda \in \C$ vlastní číslo matice $A \in \R^{n \times n}$ pak i komplexně sdružené $\overline{\lambda}$ je vlastním číslem $A$

Tvrzení

Buď $A \in \C^{n \times n}$. Je-li $A$ regulární, pak

$$A^{-1} \in span\{I_{n}, A, \ldots, A^{n-1}\}$$

Tedy $A^{-1}$ je lineární kombinací matic $I_{n}, A, \ldots, A^{n-1}$.

Důkaz

Víme, že $A^{-1} = (-1)^{n}A^{n} + \alpha_{n-1}A^{n-1} + \ldots + \alpha_{1}A + \alpha_{0} I_{n} = 0$
Také víme, že $\alpha_{0} = \det(A) \neq 0$.

$$I = -\frac{(-1)^{n}}{\alpha_{0}}A^{n} - \frac{\alpha_{n}-1}{\alpha_{0}}A^{n-1} + \ldots + -\frac{\alpha_{1}}{\alpha_{0}}A =\\ A\left(-\frac{(-1)^{n}}{\alpha_{0}}A^{n-1} - \frac{\alpha_{n}-1}{\alpha_{0}}A^{n-2} + \ldots + -\frac{\alpha_{1}}{\alpha_{0}}I_{n}\right)$$

Vynásobíme $A^{-1}$

$$A^{-1} = -\frac{(-1)^{n}}{\alpha_{0}}A^{n-1} - \frac{\alpha_{n-1}}{\alpha_{0}}A^{n-2}-\ldots - \frac{\alpha_{1}}{\alpha_{0}}I_{n}$$

Dá se díky tomu částečně dobře spočítat výsledek s nízkým počtem matic.

Definice

Matice $A,B \in \C^{n \times n}$ jsou podobné, pokud existují regulární $S \in \C^{n \times n}$ tak, že

$$A = SBS^{-1} \equiv AS=SB$$

Věta

Podobné matice mají stejná vlastní čísla

Důkaz

$A = SBS^{-1}\\ \\ P_{A}(\lambda) = \\ \det(A - \lambda I_{n}) = \\ \det(SBS^{-1} - \lambda SIS^{-1}) = \\ \det\left( S \left( B - \lambda I_{n} \right) S^{-1} \right) = \\ \det(S) \cdot \det(B - \lambda I_{n}) \cdot \det(S^{-1}) = \\ \det(B - \lambda I_{n}) = P_{B}(\lambda)$$$

Tvrzení

Nechť $A,B,C \in \C^{n \times n}$ jsou podobné a $\lambda$ je jejich vlastní číslo. Pak počet vlastních vektorů pro $\lambda$ je stejný u obou matic.

Důkaz

$A = SBS^{-1}$
$dim(Ker(A-\lambda I_{n})) = n - rank(A- \lambda I_{n})$
$rank(A - \lambda I_{n}) = rank(SBS^{-1} - \lambda I_{n}) = rank(S(B-\lambda I_{n})S^{-1}) = rank(B - \lambda I_{n})$

Definice

Spektrum a spektrální poloměr

Nechť $A \in \C^{n \times n}$ má vlastní čísla $\lambda_{1}, \ldots, \lambda_{n}$. Pak

• Spektrum matice a je množina vlastních čísel $\{\lambda_{1}, \ldots, \lambda_{n}\}$
• Spektrální poloměr je $p(A) = \max_{i= 1, \dots, n} \lvert \lambda_{i} \rvert$

Definice

Matice společnice

Buď $p(x) = x^{n} + a_{n-1}x{n-1}+ \ldots + a_{1}x + a_{0}$. Pak matice společnice polynomu $p(x)$ je čtvercová matice řádu $n$ definovaná

$$C(p) := \left( {\begin{array}{ccccc} 0 & 0 & \cdots & 0 & -a_{0} \\ 1 & 0 & \cdots & 0 & -a_{1} \\ 0 & 1 & \cdots & 0 & -a_{2} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & -a_{n-1} \end{array} } \right)$$

Věta

Věta o matici společnici

Platí $P_{c_{(p)}}(\lambda) = (-1)^{n}p(\lambda)$.
Tedy vlastní čísla matice $C(p)$ odpovídají kořenům polynomu $P(\lambda)$.

Diagonalizovatelnost

Definice

Matice $A \in \C^{n \times n}$ je diagonalizovatelná, pokud její podobná nějaká diagonální matici.

Věta

Charakterizace diagonalizovatelnosti

Matice $\in \C^{n \times n}$ je diagonalizovatelná právě tehdy, když má $n$ lineárně nezávislých vlastních vektorů.

Důkaz

$A = S\Lambda S^{-1} \implies AS = S\Alpha$$$

$$AS_{*~j} = (AS)_{*~j} = SA_{*~j}=SA_{j~j}e_{j} = \Lambda_{j~j}S_{*~j}$$

Vlastnosti diagonalizovatelných matic

• Algebraická a geometrická násobnost vlastních čísel je stejná
• Hodnost matice $A$ je rovna počtu nenulových vlastních čísel $A$

Tvrzení

Je-li $A-S\Lambda S^{-1}$ spektrální rozklad matice $A$, pak

$$A^{T} = S{-T}\Lambda S^{T}$$

Tvrzení

Buďte $\lambda_{1}, \ldots, \lambda_{n}$ navzájem různá čísla matice $A \in \C^{n \times n}$. Pak odpovídající vlastní vektory $x_{1},\ldots,x_{n}$ jsou lineárně nezávislé.

Důkaz

Matematickou indukcí.

Důsledek

Pokud matice $A \in \C^{n \times n}$ má $n$ navzájem různých vlastních čísel, pak je diagonalizovatelná.

Definice

Jordanova buňka

Buď $\lambda \in \C, k \in \N$. Jordánova buňka $J_{k}(\lambda)$ je čtvercová matice řádu $k$ definovaná jako

$$J_{k}(\lambda) := \left( {\begin{array}{ccccc} \lambda & 1 & 0 & \cdots & 0 \\ 0 & \lambda & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ 0 & 0 & 0 & \lambda & 1 \\ 0 & 0 & 0 & 0 & \lambda \end{array} } \right)$$

Jordánova buňka má vlastní číslo $\lambda$, které je $k$-násobné a přísluší mu pouze jednotkový vektor $e=(1,0,\ldots,0)^{T}$

Definice

Jordánova normální forma

Matice $J \in \C^{n \times n}$ je v Jordánově normální formě, pokud je v blokově diagonálním tvaru.

$$J = \left( {\begin{array}{ccccc} J_{k_{1}}(\lambda_{1}) & 0 & 0 & \cdots & 0 \\ 0 & J_{k_{2}}(\lambda_{2}) & \ddots & \ddots & \vdots \\ \vdots & 0 & \ddots & \ddots & 0 \\ \vdots & \vdots & \ddots & \ddots & 0 \\ 0 & 0 & \cdots & 0 & J_{k_{n}}(\lambda_{n}) \end{array} } \right)$$

a na diagonále jsou Jordánovy buňky $J_{k_{1}}(\lambda_{1}),J_{k_{2}}(\lambda_{2}), \ldots, J_{k_{n}}(\lambda_{n})$. Pokud všechny Jordanovy buňky mají velikost 1, matice je diagonální.

Věta

Každá matice $A \in \C^{n \times n}$ je podobná matici v Jordánově normální formě. Tato matice je až na pořadí buněk určena přesně.

Důsledek

Počet všech Jordánových buněk odpovídajících $\lambda$ je roven počtu vlastních vektorů pro $\lambda$.

Násobnost vlastního čísla je větší nebo rovna počtu vlastních vektorů, které mu přísluší.

Poznámka

Počet buněk $J_{k}(\lambda)$ matice $A \in \C^{n \times n}$ ve výsledné Jordánově normální formě je roven $rank(\widetilde{A}^{k-1}) -2rank(\widetilde{A}^{k}) + rank(\widetilde{A}^{k+1})$ kde $\widetilde{A} = A - \lambda I_{n}$

Příklad matice v Jordanově normální formě

Buď $A \in \R{5 \times 5}$ a nechť $rank(A-BI_{5}) = 3$
Jordanova buňka pro vlastní číslo $8$ je $5-3=2$
$rank((A -BI_{5})^{2}) = rank((A-BI_{5})^{3})=2$ $\implies$ jedna buňka velikosti $1$ a jedna velikost $2$

Definice

Polynomiální matice a maticový polynom

$$\begin{pmatrix} \lambda^{2}-\lambda & 2\lambda-3 \\ 7 & 5\lambda^{2}-4 \end{pmatrix} = \lambda^{2} \begin{pmatrix} 1 & 0 \\ 0 & 5 \end{pmatrix} + \lambda \begin{pmatrix} -1 & 2 \\ 0 & 0 \end{pmatrix} + \begin{pmatrix} 0 & -3 \\ 7 & -4 \end{pmatrix}$$

Příklad mocninné matice

Buď $A=SJS^{-1}$ Jordánůva normální forma matice $A \in \C^{n \times n}$. Pak

$$A^{k} = SJ^{k}S^{-1}$$

$J$ je blokově diagonální $\implies$ stačí mocnit Jordanovy buňky.

$$\lim_{k \rightarrow \infty} A^{k} = \begin{cases} 0 & p(A) < 1 \\ \text{diverguje} & p(A) > 1 \\ \text{konverguje} & p(A) = 1 \end{cases}$$

Definice

Hermitovská matice a transpozice

Hermitovská transpozice matice $A \in \C^{n \times n}$ je matice $A^{*} := A^{-T}$. Matice $A \in \C^{n \times n}$ se nazývá hermitovská, pokud $A^{*} = A$

Pokud je $A$ reálná $\implies A^{*}=A^{T}$.(Chová se stejně jako normální transpozice)

Věta

Vlastní čísla reálných symetrických matic jsou reálná.

Důkaz

Buď $A \in \C^{n \times n}$ hermitovské, $\lambda \in \C$ její vlastní čísla a $x \in \C^{n}$ přísluší vlastnosti vektor.

$$\begin{align*} Ax &= \lambda x / x^{*} \\ x^{*} &= \lambda x^{*}x = \lambda \\ \lambda^{2} = x^{*}Ax &= x^{*}A^{*}x = \lambda^{*} \\ \lambda &= \overline{\lambda} \end{align*}$$

A to platí jen pro $\lambda \in \R$

Věta

Buď $A \in \C^{n \times n}$ a

$$P_{A}(\lambda) = \det(A -\lambda I_{n}) = (-1)^{n}\lambda^{n} + \alpha_{n-1}\lambda^{n-1}+\ldots+\alpha_{1}\lambda + \alpha_{0}$$

Pak

$$(-1)^{n}A^{n} + \alpha_{n-1}A^{n-1}+\ldots+\alpha_{1}A + \alpha_{0}I_{n} \implies P_{A}(A) = 0$$

Důkaz

Víme, že $(A -\lambda I_{n}) adj(A-\lambda I_{n}) = \det(A-\lambda I_{n})I_{n}$ a $adj(A - \lambda I_{n}) = \lambda^{n-1}B_{n-1} + \ldots + \lambda B_{1} + B_{0}$ pro určité $B_{i}$.

Dosazením

$$(A - \lambda I_{n})(\lambda^{n-1}B_{n-1} + \ldots + \lambda B_{1} + B_{0}) =\\ (-1)^{n}\lambda^{n} + \alpha_{n-1}\lambda^{n-1} + \ldots + \alpha_{1}\lambda + \alpha_{0})I_{n}$$

vznikne

$$-B_{n-1}\lambda^{n} + (AB_{n-1} - B_{n-2})\lambda^{n-1} + \ldots + (AB_{1} - B_{0})\lambda + AB_{0} = \\ (-1)^{n}\lambda^{n}I_{n}+a_{n-1}\lambda^{n}I_{n} + \alpha_{n-1}\lambda{n-1} + \ldots + \alpha_{1}\lambda I_{n} + \alpha_{0}I_{n}$$

Porovnáme koeficient

$$\begin{align*} -B_{n-1} &= (-1)^{n}I_{n} \\ AB_{j}-B &= \alpha_{j}I_{n} \text{ pro } j=1,\ldots,n \\ AB_{0} &= \alpha_{0}I_{n} \end{align*}$$

Vynásobíme postupně rovnice prvním $A^{n}$ poslední $A^{0}$. Sečteme a vyjde nám

$$0 = (-1)^{n}A^{n} + \alpha_{n-1}A^{n-1}+\ldots+\alpha_{1}A+\alpha_{0}I_{n}$$

Tvrzení

Důsledek

Buď $A \in \C^{n \times n}$. Pak pro každé $k \in \N$ je

$$A^{k} \in span\{I_{n}, A, \ldots, A^{n+1}\}$$

tedy je jejich lineární kombinací.

Důkaz

Stačí uvažovat $k \geq n$
Vydělíme $\lambda^{k}$ polynomem $P_{A}(\lambda)$
$\lambda^{k} = r(\lambda) P_{A}(\lambda)+S(\lambda)$
kde $S(\lambda)$ je zbytek $b_{n-1}\lambda^{n-1}+\ldots+b_{1}\lambda+b_{0}$ s dosazením matic

$$A^{k} = \underbrace{r(A)P_{A}(A)}_{=0}+ S(A) = S(A)$$

Positivně (semi-)definitní matice

Definice

Buď $A \in \R^{n \times n}$ symetrická/ Pak $A$ je positivně semi-definitní, pokud $x^{T}Ax \geq 0$ pro všechna $x \in \R^{n}$ a je positivně defitní pokud $x^{T}A > 0$ pro všechna $x \neq 0$

Definice se dá zobecnit i pro nesymetrické matice.

$$x^{T}\frac{1}{2}\left(A + A^{T}\right)x= \frac{1}{2}x^{t}\left(A+A^{T}\right)x = \frac{1}{2}x^{T}Ax + \left(\frac{1}{2}x^{T}Ax\right)^{T} = x^{T}Ax$$

Pozorování

Pozitivně semidefinitní matice má nezápornou diagonálu, pozitivně definitní matice má kladnou diagonálu.

Tvrzení

1. Jsou-li $A,B \in \R^{n \times n}$ positivně definitní, pak i $A+B$ je positivně definitní.
2. Je-li $A \in \R^{n \times n}$ positivně definitní a $\alpha > 0$, pak i $\alpha A$ je positivně definitní
3. Je-li $A \in \R^{n \times n}$ positivně definitní, pak je regulární a $A^{-1}$ je positivně definitní.

Poznámka

Semi-definitivní matice nemusí být regulární

Věta

Buď $A \in \R^{n \times n}$ symetrická. Pak následující podmínky jsou ekvivalentní.

1. $A$ je positivně definitivní
2. vlastní čísla $A$ jsou kladná
3. existuje matice $U \in \R^{m \times n}$ hodnosti $n$ taková, že $A=U^{T}U$

Věta

Charakterizace semi-definitní

1. $A$ je semidefitní
2. vlastní čísla $A$ jsou nezáporná
3. existuje matice $U \in \R^{m \times n}$ taková, že $A = U^{T}U$

Věta

Nechť $A \in \R^{n \times n}$ je symetrická. Řekněme, že $A'$ je hlavní podmatice $A$ jestliže $A'$ vznikne z $A$ odstraněním podmnožiny řádků a sloupců se stejnými indexy.

Lemma

$A$ je positivně definitní právě tehdy když každá hlavní podmatice $A$ je positivně definitní.

Věta

Cholevského rozklad

Pro každou positivně definitní matici $A \in \R^{n \times n}$ existuje jediná dolní trojúhelníková matice $L \in \R^{n \times n}$ s kladnou diagonálou taková, že $A=LL^{T}$.