MATFYZ

Natural language processing

June 10 2024 [Edit]

• Probability
  • Experiments & Sample Spaces
  • Events
  • Probability
  • Estimating probability
  • Example
  • Basic Properties
  • Joint and Conditional Probability
  • Bayes Rule
  • Independence
  • Chain Rule
  • Bayesian Network
  • Total Probability Law
  • Normalization
  • Markov Assumption

Probability

Experiments & Sample Spaces

• Experiment, process, test, …
• Set of possible basic outcomes: sample space $\Omega$
• coin toss $(\Omega=\{\text{head, tail}\})$, die $(\Omega=\{1, \ldots, 6\})$
• yes/no opinion poll, quality test (bad/good) $(\Omega=\{0, 1\})$
• lottery $\left(\lvert \Omega \rvert \cong 10^{7} \ldots 10^{12}\right)$
• $\#$ of traffic accidents somewhere per year $(\Omega=\N)$
• spelling errors ( $\Omega=Z^{*}$ ), where $\Z$ is an alphabet, and $Z^{*}$ is a set of possible strings over such an alphabet
• missing word $(\lvert \Omega \rvert \cong \text{vocabulary size })$

Events

• Event $\mathrm{A}$ is a set of basic outcomes
• Usually $\mathrm{A} \subseteq \Omega$, and all $\mathrm{A} \in 2^{\Omega}$ (the event space)
• $\Omega$ is then the certain event, $\varnothing$ is the impossible event
• Example:
  • experiment: three times coin toss
  • $\Omega=\{\mathrm{HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}\}$
  • count cases with exactly two tails: then $\mathrm{A}=\{\mathrm{HTT, THT, TTH}\}$
  • all heads: $\mathrm{A} = \{\mathrm{HHH}\}$

Probability

• Repeat experiment many times, record how many times a given event $A$ occurred (“count” $\mathrm{c}_{1}$ ).
• Do this whole series many times; remember all $\mathrm{c}_{\mathrm{i}}$.
• Observation: if repeated really many times, the ratios of $\mathbf{c}_{i} / T_{i}$ (where $T_{i}$ is the number of experiments run in the $i$-th series) are close to some (unknown but) constant value.
• Call this constant a probability of $A$. Notation: $\mathbf{p(A)}$

Estimating probability

• Remember: … close to an unknown constant.
• We can only estimate it:
  • from a single series (typical case, as mostly the outcome of a series is given to us and we cannot repeat the experiment), set

$$\mathrm{p}(\mathrm{A})=\mathrm{c}_{1} / \mathrm{T}_{1}.$$

• otherwise, take the weighted average of all $c_{i} / T_{i}$ (or, if the data allows, simply look at the set of series as if it is a single long series).
• This is the best estimate.

Example

• Recall our example:
  • experiment: three times coin toss
  • $\Omega=\{\mathrm{HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}\}$
  • count cases with exactly two tails: $\mathrm{A}=\{\mathrm{HTT, THT, TTH}\}$
  • Run an experiment 1000 times (i.e. 3000 tosses)
  • Counted: 386 cases with two tails (HTT, THT, or TTH)
  • estimate: $\mathrm{p}(\mathrm{A})=386 / 1000=.386$
  • Run again: 373, 399, 382, 355, 372, 406, 359

$$\mathrm{p}(\mathrm{A})=.379 \text{ (weighted average) or simply } 3032 / 8000$$

• Uniform distribution assumption: $\mathrm{p}(\mathrm{A})=3 / 8=.375$

Basic Properties

• Basic properties:
  • p: $2^{\Omega} \rightarrow [0,1]$
  • $\mathrm{p}(\Omega)=1$
  • Disjoint events: $\mathrm{p}\left(\cup \mathrm{A}_{\mathrm{i}}\right)=\sum_{\mathrm{i}} \mathrm{p}\left(\mathrm{A}_{\mathrm{i}}\right)$
  • [NB: axiomatic definition of probability: take the above three conditions as axioms]
  • Immediate consequences:

$$\begin{aligned} p(\varnothing) &= 0 \\ p(\bar{A}) &= 1-p(A), \quad A \subseteq B \Rightarrow p(A) \leq p(B) \\ \sum_{a \in \Omega} p(a) &= 1 \\ \end{aligned}$$

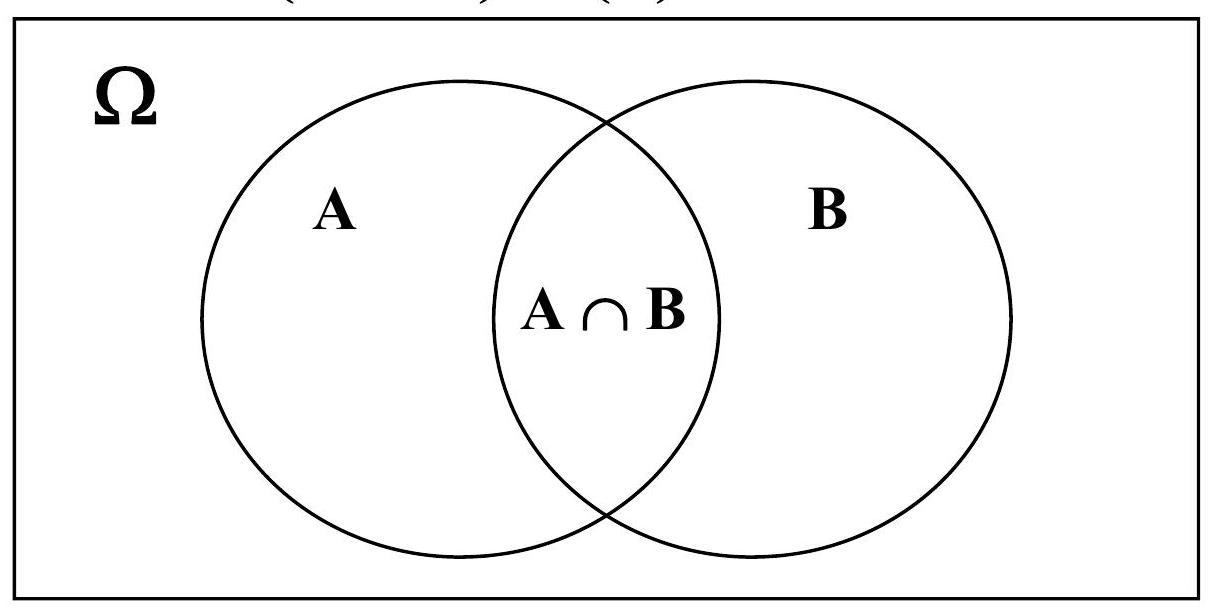
Joint and Conditional Probability

$$\mathrm{p}(\mathrm{A}, \mathrm{B})=\mathrm{p}(\mathrm{A} \cap \mathrm{B})$$ $$\mathrm{p}(\mathrm{A} \mid \mathrm{B})=\mathrm{p}(\mathrm{A}, \mathrm{B}) / \mathrm{p}(\mathrm{B})$$

Estimating from counts:

$$\mathbf{p}(\mathbf{A} \mid \mathrm{B})= \mathbf{p}(\mathbf{A}, \mathrm{B}) / \mathbf{p}(\mathrm{B})= (\mathbf{c}(\mathbf{A} \cap B) / T) /(\mathbf{c}(\mathrm{B}) / T)= \mathbf{c}(\mathbf{A} \cap \mathbf{B}) / \mathbf{c}(\mathbf{B})$$

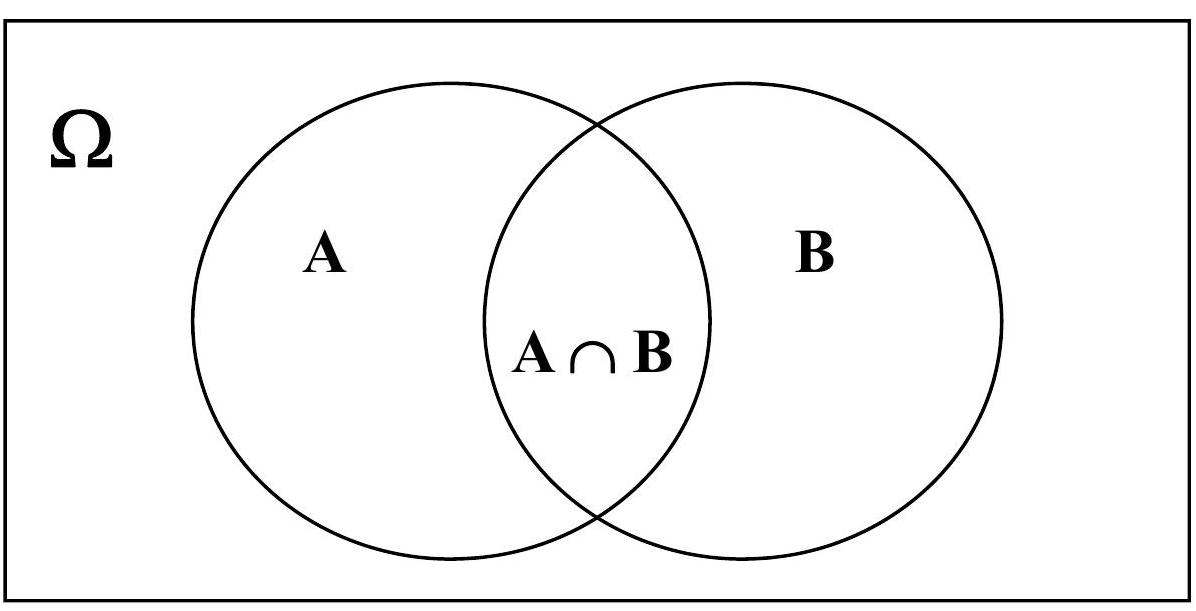
Bayes Rule

$$p(A, B)=p(B, A)$$

since

$$p(A \cap B)=p(B \cap A)$$

therefore

$$\mathrm{p}(\mathrm{A} \mid \mathrm{B}) \mathrm{p}(\mathrm{B})=\mathrm{p}(\mathrm{B} \mid \mathrm{A}) \mathrm{p}(\mathrm{A})$$

and therefore

$$\mathrm{p}(\mathrm{A} \mid \mathrm{B})=\mathrm{p}(\mathrm{B} \mid \mathrm{A}) \mathrm{p}(\mathrm{A}) / \mathrm{p}(\mathrm{B})$$

Independence

• Can we compute $\mathrm{p}(\mathrm{A}, \mathrm{B})$ from $\mathrm{p}(\mathrm{A})$ and $\mathrm{p}(\mathrm{B})$?
• Recall from previous foil:

$$\begin{aligned} \mathrm{p}(\mathrm{A} \mid \mathrm{B}) & =\mathrm{p}(\mathrm{B} \mid \mathrm{A}) \mathrm{p}(\mathrm{A}) / \mathrm{p}(\mathrm{B}) \\ \mathrm{p}(\mathrm{A} \mid \mathrm{B}) \mathrm{p}(\mathrm{B}) & =\mathrm{p}(\mathrm{B} \mid \mathrm{A}) \mathrm{p}(\mathrm{A}) \\ \mathrm{p}(\mathrm{A}, \mathrm{B}) & =\mathrm{p}(\mathrm{B} \mid \mathrm{A}) \mathrm{p}(\mathrm{A}) \end{aligned}$$

… we’re almost there: how $\mathrm{p}(\mathrm{B} \mid \mathrm{A})$ relates to $\mathrm{p}(\mathrm{B})$?

$\mathrm{p}(\mathrm{B} \mid \mathrm{A})=\mathrm{p}(\mathrm{B})$ (iff $\mathrm{A}$ and $\mathrm{B}$ are independent)

• Example: two coin tosses, weather today and weather on March 4th, 1789;
• Any two events for which $\mathrm{p}(\mathrm{B} \mid \mathrm{A})=\mathrm{p}(\mathrm{B})$!

Chain Rule

$\mathrm{p}\left(\mathrm{A}_{1}, \mathrm{A}_{2}, \mathrm{A}_{3}, \mathrm{A}_{4}, \ldots, \mathrm{A}_{\mathrm{n}}\right)=$

$$\mathrm{p}\left(\mathrm{A}_{1} \mid \mathrm{A}_{2}, \mathrm{A}_{3}, \mathrm{A}_{4}, \ldots, \mathrm{A}_{\mathrm{n}}\right) \times \mathrm{p}\left(\mathrm{A}_{2} \mid \mathrm{A}_{3}, \mathrm{A}_{4}, \ldots, \mathrm{A}_{\mathrm{n}}\right) \times$$ $$\times \mathrm{p}\left(\mathrm{A}_{3} \mid \mathrm{A}_{4}, \ldots, \mathrm{A}_{\mathrm{n}}\right) \times \ldots \times \mathrm{p}\left(\mathrm{A}_{\mathrm{n}-1} \mid \mathrm{A}_{\mathrm{n}}\right) \times \mathrm{p}\left(\mathrm{A}_{\mathrm{n}}\right)$$

• Also applicable for conditional probabilities.
• Basic idea: instead of estimating a complex joint distribution, break it up into the products of simpler conditional distributions.

Bayesian Network

• A Bayesian network (or belief network) is a graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG).

Total Probability Law

• Sum up conditional probabilities:

$$\mathrm{p}(\mathrm{A})=\sum_{\mathrm{i}} \mathrm{p}(\mathrm{A}, \mathrm{B}_{\mathrm{i}})=\sum_{\mathrm{i}} \mathrm{p}(\mathrm{A} \mid \mathrm{B}_{\mathrm{i}}) \mathrm{p}(\mathrm{B}_{\mathrm{i}})$$

Normalization

• Let’s sum up over all possible outcomes:

$$\begin{aligned} \mathrm{p}(\Omega) & =1 \\ \sum_{\omega} \mathrm{p}(\omega) & =1 \\ \sum_{\omega} \mathrm{p}(\omega \mid \mathrm{B}) \mathrm{p}(\mathrm{B}) & =1 \quad \text { for any B } \\ \sum_{\omega} \mathrm{p}(\omega \mid \mathrm{B}) & =1 \quad \text { for any B } \end{aligned}$$

• i.e. conditional probabilities of a variable given a value of another variable sum up to 1.

Markov Assumption

• Graphical representations of $\mathrm{p}\left(\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots, \mathbf{x}_{\mathbf{n}}\right)$ often decompose the overall distribution into locally conditioned distributions.
• Simplest decomposition (often very accurate for natural processes): the value of $\mathrm{x}_{\mathrm{t}}$ is (conditionally) dependent only on the value of $\mathbf{x}_{\mathrm{t}-1}$, i.e.

$$\mathrm{p}\left(\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots, \mathbf{x}_{\mathbf{n}}\right)=\mathrm{p}\left(\mathbf{x}_{1}\right) \prod_{\mathrm{t}=2}^{\mathrm{n}} \mathrm{p}\left(\mathbf{x}_{\mathrm{t}} \mid \mathbf{x}_{\mathrm{t}-1}\right)$$

• (this is often called the first order Markov model or Markov chain)
• $N$-th order Markov models: $\mathrm{x}_{\mathrm{t}}$ conditionally dependent on $\mathrm{x}_{\mathrm{t}-1}, \mathbf{x}_{\mathrm{t}-2}, \ldots, \mathrm{x}_{\mathrm{t}-\mathrm{n}}$ :

$$\mathrm{p}\left(\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots, \mathbf{x}_{\mathbf{n}}\right)=\mathrm{p}\left(\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots, \mathbf{x}_{\mathbf{n}}\right) \prod_{\mathrm{t}=\mathrm{n}+1}^{\mathrm{T}} \mathrm{p}\left(\mathbf{x}_{\mathrm{t}} \mid \mathbf{x}_{\mathrm{t}-1}, \mathbf{x}_{\mathrm{t}-2}, \ldots, \mathrm{x}_{\mathrm{t}-\mathrm{n}}\right)$$